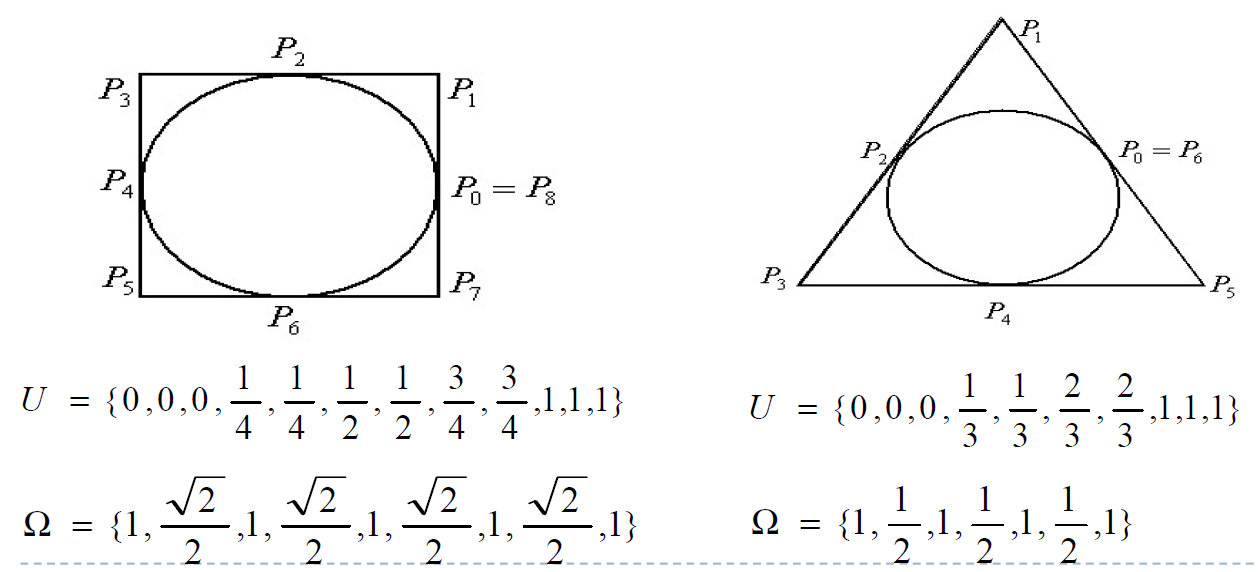目录:
NURBS曲线
NURBS曲线(非均匀有理B样条)是由分段有理B样条多项式基函数定义的,k阶NURBS曲线的定义如下:
$P(t)=\frac{\sum_{i=0}^{n}w_{i}P_{i}N_{i,k}(t)}{\sum_{i=0}^{n}w_{i}N_{i,k}(t)}=\sum_{i=0}^{n}P_{i}R_{i,k}(t)$
$R_{i,k}(t)=\frac{w_{i}N_{i,k}(t)}{\sum_{j=0}^{n}w_{j}N_{j,k}(t)}$
NURBS曲线的性质
$R_{i,k}(t)$具有k阶B样条基函数类似的性质
- 局部支撑性:$R_{i,k}(t)=0$, $t\notin [t_{i},t_{i+k}]$
- 权性:$\sum_{i=0}^{n}R_{i,k}(u)=1$
- 可微性:如果分母不为零,在节点区间内是无限次连续可微的,在节点处(k-1-r)次连续可导,r是该节点的重复度
NURBS曲线与B样条曲线具有类似的几何性质
- 局部性质
- 局变差减小性质
- 凸包性
- 在仿射与透射变换下的不变性
- 在曲线定义域内有与有理基函数同样的可微性
- 如果某个权因子为零,那么相应控制顶点对曲线没有影响
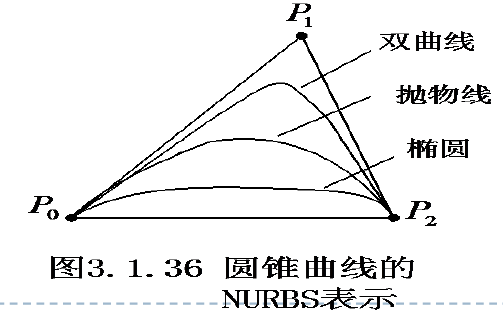
圆锥曲线的NURBS表示
取节点向量$T=[0,0,0,1,1,1]$,为则NURBS曲线退化为二次Bézier曲线,且可以证明,这是圆锥曲线弧方程。
$P(t)=\frac{(1-t^2)w_{0}P_{0}+2t(1-t)w_{1}P_{1}+t^2w_{2}P_{2}}{(1-t^2)w_{0}+2t(1-t)w_{1}+t^2w_{2}}$
其中,$C_{sf}=\frac{w_{1}^2}{w_{0}w_{2}}$ 称为形状因子,$C_{sf}$ 的值确定了圆锥曲线的类型
$C_{sf}=1$ 时,上式是抛物线弧
$C_{sf}\in(1,\infty)$ 时,上式是双曲线弧
$C_{sf}\in(0,1)$ 时,上式是椭圆弧
$C_{sf}=0$ 时,上式退化为一对直线段P0P1和P1P2
$C_{sf}\rightarrow+\infty$ 时,上式退化为连接两点P0P2的直线段
NURBS曲线的修改
常用的方法有修改权因子、控制点和反插节点
- 修改权因子: 当保持控制顶点和其它权因子不变,减少或增加某权因子时,曲线被推离或拉向相应顶点
- 修改控制顶点: 修改控制顶点的位置,曲线随之变形
- 反插节点法
NURBS曲面
定义
$P(u,v)=\frac{\sum_{i=0}^{m}\sum_{j=0}^{n}w_{ij}P_{ij}N_{i,p}(u)N_{j,q}(v)}{\sum_{i=0}^{m}\sum_{j=0}^{n}w_{ij}N_{i,p}(u)N_{j,q}(v)}=\sum_{i=0}^{m}\sum_{j=0}^{n}P_{ij}R_{i,p;j,q}(u,v)$, $u,v\in[0,1]$
$R_{i,p;j,q}(u,v)=\frac{w_{ij}N_{i,p}(u)N_{j,q}(v)}{\sum_{r=0}^{m}\sum_{s=0}^{n}w_{rs}N_{r,p}(u)N_{s,q}(v)}$
规定四角点处用正权因子,即$w_{00},w_{m0},w_{0n},w_{mn}>0$,其余$w_{ij}≥0$
性质
与非有理B样条基函数相类似的性质:
- 局部支承性质
- 权性
- 可微性:在重复度为 $r$ 的 $u$ 节点处沿 $u$ 向是 $p-r-1$ 次连续可微,在重复度为 $r$ 的 $v$ 节点处沿 $v$ 向是 $q-r-1$ 次连续可微
- 极值.若 $p,q>1$,恒有一个极大值存在
- 是双变量B样条基函数的推广