目录：

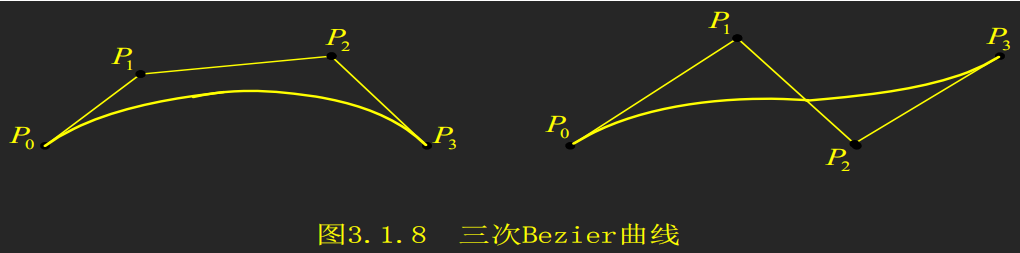
Bézier曲线

定义

给定空间n+1个点的位置矢量Pi(i=0,1,2...)，则Bezier参数曲线上各点坐标的插值公式是：$P(t)=\sum_{i=0}^{n}P_{i}B_{i,n}(t), t\in [0,1]$

其中，Pi构成该贝塞尔曲线的特征多边形，$B_{i,n}(t)$是n次Bernstein基函数：
$B_{i,n}(t) = C_{i}^{n}t^{i}(1-t)^{n-i} = \frac{n!}{i!(n-i)!}t^{i}\cdot (1-t)^{n-i} (i=0,1,...,n)$

非负性：$B_{i,n}(t)≥0, t\in [0,1]$
端点性质
$B_{i,n}(0) = \begin{cases} 1 & (i=0) \\ 0 & otherwise \end{cases}$ $B_{i,n}(1) = \begin{cases} 1 & (i=n) \\ 0 & otherwise \end{cases}$
权性
$\sum_{i=0}^{n}B_{i,n}(0) = \sum_{i=0}^{n}C_{n}^{i}t^{i}(1-t)^{n-i}=[(1-t)+t]^{n}\equiv 1$
对称性
$B_{i,n}(t) = B_{n-i,n}(1-t)$
因为
$B_{n-i,n}(1-t) = C{n}^{i}$
递推性
$B_{i,n}(t) = (1-t)B_{i,n-1}(t) + tB_{i-1,n-1}(t) (i=0,1,...,n)$
即高一次的Bernstein基函数可由两个低一次的Bernstein调和函数线性组合而成, 因为$C_{n}^{i} = C_{n-1}^{i} + C_{n-1}^{i-1}$
导函数
$B'n(t) = n[B_{i-1,n-1}(t)-B_{i,n-1}(t)] (i=0,1,...,n)$
最大值
$B_{i,n}(t)$在 $t = \frac{i}{n}$ 处达到最大值
升阶公式
$(1-t)B_{i,n}(t)=(1-\frac{i}{n+1})B_{i,n+1}(t)$
$tB_{i,n}(t)=\frac{i+1}{n+1}B_{i+1,n+1}(t)$
$B_{i,n}(t)=(1-\frac{i}{n+1})B_{i,n+1}(t)+\frac{i+1}{n+1}B_{i+1,n+1}(t)$
积分 $\int_{0}^{1}B_{i,n}(t) = \frac{1}{n+1}$

端点性质
- 曲线端点位置矢量
  由Bernstein基函数的端点性质可以推得，当t=0时，P(0)=P0 ；当t=1时，P(1)=Pn。由此可见，Bézier曲线的起点、终点与相应的特征多边形的起点、终点重合。
- 切矢量
  因为$P'(t) = n\sum_{i=0}^{n-1}P_{i}[B_{i-1,n-1}(t) - B_{i,n-1}(t)]$
  所以当t=0时，P'(0)=n(P1-P0)，当t=1时，P'(1)=n(Pn-Pn-1)，这说明Bézier曲线的起点和终点处的切线方向和特征多边形的第一条边及最后一条边的走向一致。
对称性：由控制顶点构造出的新Bézier曲线，与原Bézier曲线形状相同，走向相反。
这个性质说明Bézier曲线在起点处有什么几何性质，在终点处也有相同的性质。
几何不变性：是指某些几何特性不随坐标变换而变化的特性
变差缩减性：若Bézier曲线的特征多边形是一个平面图形，则平面内任意直线与C(t)的交点个数不多于该
直线与其特征多边形的交点个数，这一性质叫变差缩减性质。
此性质反映了Bézier曲线比其特征多边形的波动还小，也就是说Bézier曲线比特征多边形的折线更光顺。
仿射不变性：在仿射变换下，Bézier曲线的形式不变。

根据定义直接生成Bézier曲线(计算量较大)
$B_{i,n}(t) = C_{i}^{n}t^{i}(1-t)^{n-i} = \frac{n!}{i!(n-i)!}t^{i}\cdot (1-t)^{n-i} (i=0,1,...,n)$
1. 给出$C_{n}^{i}$的递归计算式$C_{n}^{i}=\frac{n!}{i!(n-1)!}=\frac{n-i+1}{i}C_{n}^{i-1}$, 其中n ≥ i
2. 将p(t)表示成分量坐标形式
Bézier曲线的递推算法
Bézier曲线上的任一个点(t)，都是其它相邻线段的同等比例(t)点处的连线，再取同等比例(t)的点再连线，一直取到最后那条线段的同等比例(t)处，该点就是Bézier曲线上的点(t)
de Casteljau算法几何作图

Bézier曲线次数的提高，而高次多项式又会带来计算上的困难，实际使用中，一般不超过10次。采用分段设计，然后将各段曲线相互连接起来，并在接合处保持一定的连续条件。

给定两条Bézier曲线P(t)和Q(t)，相应控制点为Pi(i=0, 1, ..., n)和Qj(j=0,1,..., m)

要使它们达到G0连续，则：Pn= Q0
要使它们达到G1连续(平面)，只要保证Pn-1，Pn=Q，Q1三点共线就行了(因为Bezier曲线的起点和终点处的切线方向和特征多边形的第一条边及最后一条边的走向一致)
要使它们达到G2连续(空间)，则保证密切平面重合，副法线向量同向且曲率连续，更准确的说是曲率矢连续

设$P_{i,j}$(i=0,1,...,m; j=0,1,...,n)为(m+1)(n+1)个空间点列，则m×n次张量积形式的Bézier曲面定义为：

$P(u,v)=\sum_{i=0}^{m}\sum_{j=0}^{n}P_{ij}B_{i,m}(u)B_{j,n}(v)$ $u,v\in [0,1]$

其中$B_{i,m}(u)=C_{m}^{i}u^{i}(1-u)^{m-i}$, $B_{j,n}(v)=C_{n}^{j}u^{i}(1-v)^{n-j}$是Bernstein基函数。依次用线段连接点列中相邻两点所形成的空间网格，称之为特征网格。

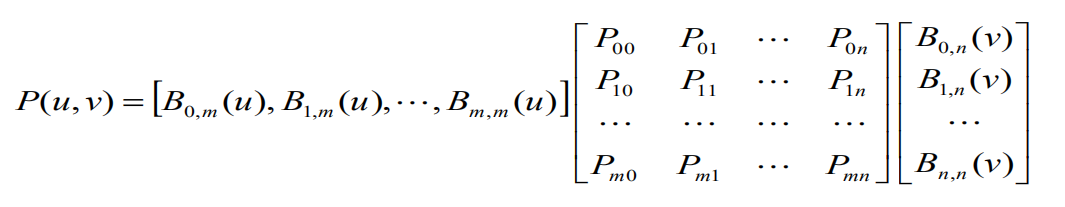
在一般应用中，n和m不大于4

角点位置：Bézier曲面特征网格的四个角点正好是Bézier曲面的四个角点，即
$P(0,0)=P_{0,0}$ $P(0,1)=P_{0,n}$
$P(1,0)=P_{m,0}$ $P(1,1)=P_{m,n}$
边界线：四条边界线也是Bézier曲线
$P(u,0)=\sum_{j=0}^{m}P_{j,0}BEZ_{j,m}(u)$ $P(v,0)=\sum_{k=0}^{n}P_{k,0}BEZ_{k,n}(v)$
$P(u,1)=\sum_{j=0}^{m}P_{j,0}BEZ_{j,m}(u)$ $P(v,1)=\sum_{j=0}^{n}P_{k,0}BEZ_{k,n}(v)$
几何不变性
对称性
凸包性

设两张m×n次Bézier曲面片

$P(u,v)=\sum_{i=0}^{m}\sum_{j=0}^{n}P_{ij}B_{i,m}(u)B_{j,n}(v)$

$Q(u,v)=\sum_{i=0}^{m}\sum_{j=0}^{n}Q_{ij}B_{i,m}(u)B_{j,n}(v)$

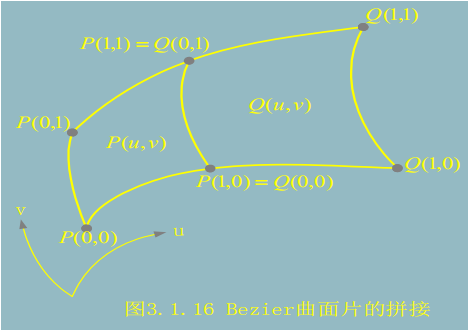
如果要求两曲面片达到$G^{0}$连续，则它们有公共的边界，即：$P(1,v)=Q(0,v)$
于是有$P_{ni}=Q_{0i}$, (i = 0, 1,..., m)

如果又要求沿该公共边界达到$G^{1}$连续，则两曲面片在该边界上有公共的切平面，因此曲面的法向应当是跨界连续的，即：
$Q_{u}(0,v)×Q_{v}(0,v)=\alpha(v)P_{u}(1,v)×P_{v}(1,v)$