目录:
直线的扫描转换算法
数值微分法(DDA)
步长=1(个象素),计算相应的y坐标y=kx+b;取象素点(x, round(y))作为当前点的坐标。
当x每递增1,y递增k(即直线斜率);
注意上述分析的算法仅适用于|k| ≤1的情形。在这种情况下,x每增加1, y最多增加1。
当 |k| > 1时,必须把x,y地位互换
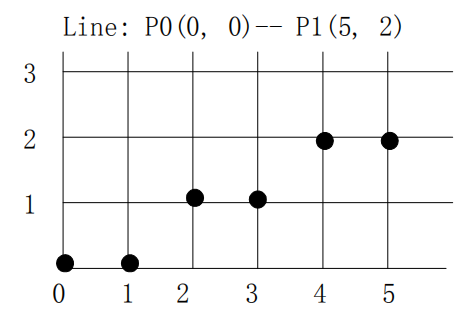
| x | round(y+0.4) | y+0.4 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0+0.4 |
| 2 | 1 | 0.4+0.4 |
| 3 | 1 | 0.8+0.4 |
| 4 | 2 | 1.2+0.4 |
| 5 | 2 | 1.6+0.4 |
中点画线法
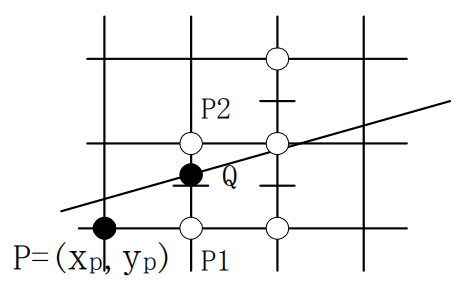
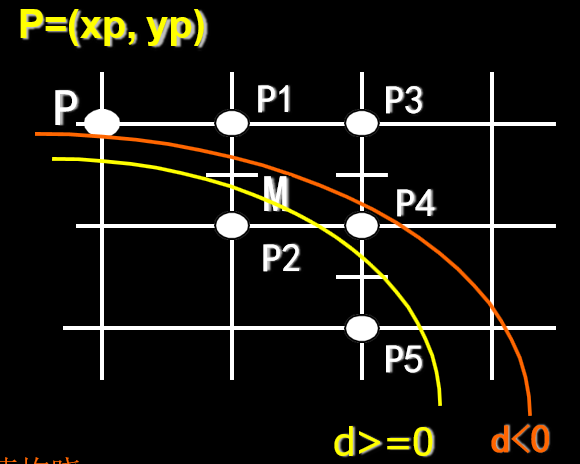
当前象素点为(xp, yp) ,下一个象素点可取为P1或P2。
设M=(xp+1, yp+0.5),为P1与P2之中点,Q为理想直线与x=xp+1垂线的交点。将Q与M的y坐标进行比较。
当M在Q的下方,则P2应为下一个象素点;
M在Q的上方,应取P1为下一点.
$a=y_{0}-y_{1}$ $b=x_{1}-x_{0}$
$c=x_{0}y_{1}-x_{1}y_{0}$
$d_{0}=2a+b$
$d_{i}=2a(x_{i}+1)+2b(y_{i}+0.5)+2c$
例:用中点画线法P0(0,0)—— P1(5,2)
$a=y_{0}-y_{1}=-2, b=x_{1}-x_{0}=5, c=0$
$d_{0}=2a+b=1,(> 0)$
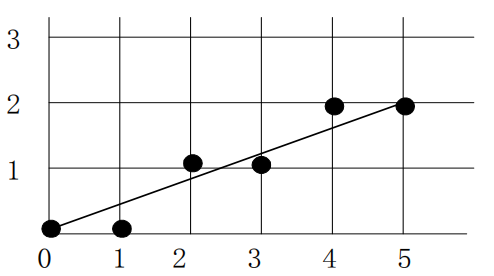
| i | xi | yi | d |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 2 | 1 | 0 | -3 |
| 3 | 2 | 1 | 3 |
| 4 | 3 | 1 | -1 |
| 5 | 4 | 2 | 5 |
Bresenham算法
设直线方程为:$y_{i+1}=y_{i}+k(x_{i+1}-x_{i})=y_{i}+k$, 其中$k=dy/dx$。
因为直线的起始点在象素中心,所以误差项d的初值$d_{0}=0$。
X下标每增加1,d的值相应递增直线的斜率值k,即$d=d+k$。一旦d≥1,就把它减去1,这样保证d在0、1之间
为方便计算,令$e=d-0.5$,e的初值为-0.5,增量为k。
当$e≥0$时,取当前象素$(x_{i},y_{i})$的右上方象素$(x_{i}+1,y_{i}+1)$;
而当$e<0$时,更接近于右方象素$(x_{i}+1,y_{i})$。
可以改用整数以避免除法。由于算法中只用到误差项的符号,因此可作替换
例:$Line$: $P_{0}(0, 0), P_{1}(5,2)$, $d=d+k$, $e$的初值为-0.5,增量为$k$, $k=\frac{dy}{dx}=0.4$

| x | y | e |
|---|---|---|
| 0 | 0 | - 0.1 |
| 1 | 0 | 0.3 |
| 2 | 1 | - 0.3 |
| 3 | 1 | 0.1 |
| 4 | 2 | - 0.5 |
| 5 | 2 | - 0.1 |
圆弧的扫描转换算法
圆的特征: 八对称性。只要扫描转换八分之一圆弧,就可以求出整个圆弧的象素集
中点画圆法
考虑中心在原点,半径为R的第二个8分圆
构造判别式(圆方程):
$d=F(M)=F(x_{p}+1,y_{p}-0.5)$
$=(x_{p}+1)^2+(y_{p}-0.5)^2-R^2$
若$d<0$,则取$P_{1}$为下一象素,而且再下一象素的判别式为
$d'=F(x_{p}+2,y_{p}-0.5)=d+2x_{p}+3$
若$d≥0$,则取$P_{2}$为下一象素,而且再下一象素的判别式为
$d'=F(x_{p}+2,y_{p}-1.5)=d=2(x_{p}-y_{p})+5$
第一个像素是(0, R),判别式d的初始值为:
$d_{0}=F(1,R-0.5)=1.25-R$
为了进一步提高算法的效率,可以将上面的算法中的 浮点数改写成整数,将乘法运算改成加法运算,即仅用整数实现中点画圆法
使用 $e=d-0.25$ 代替$d$,则 $e_{0}=1-R$