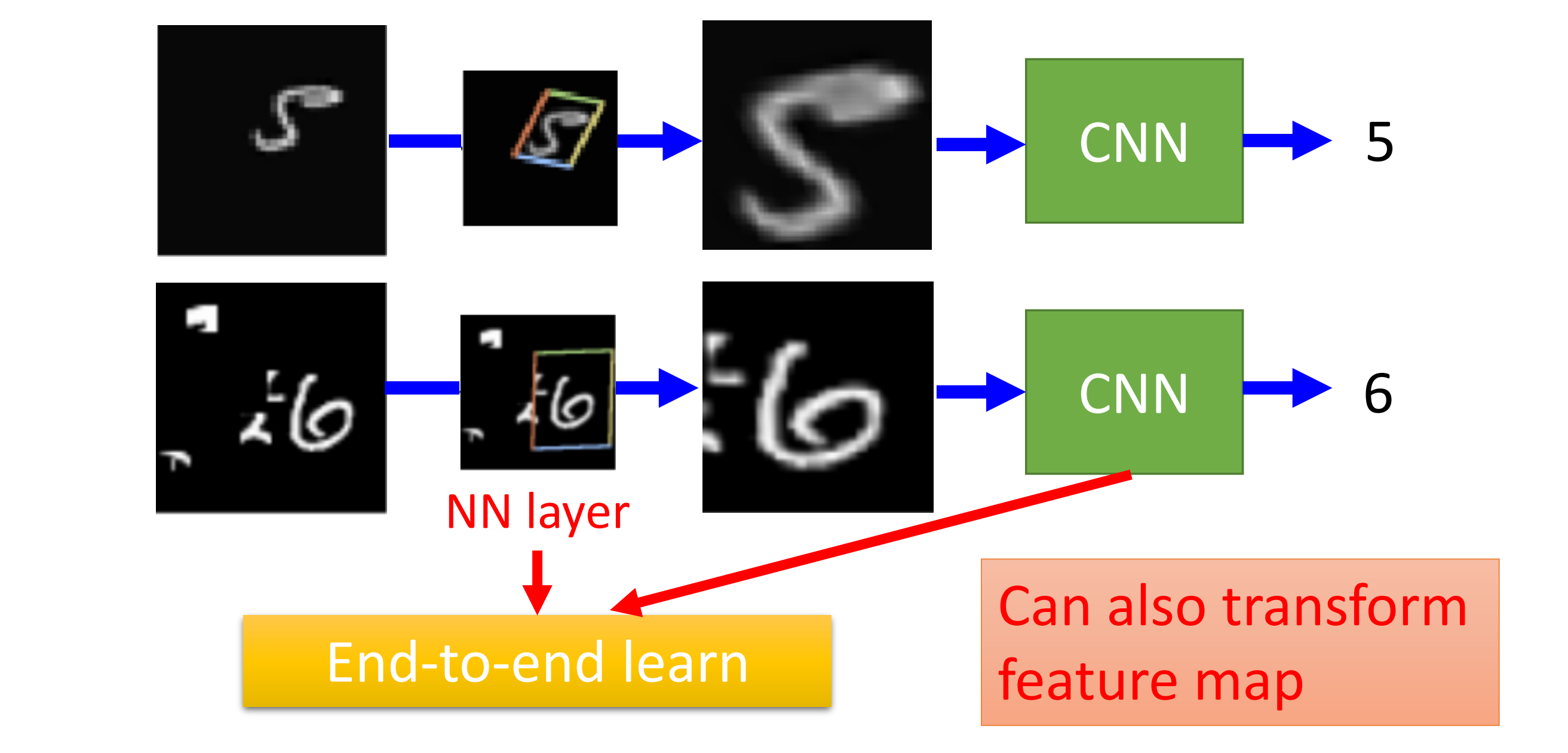
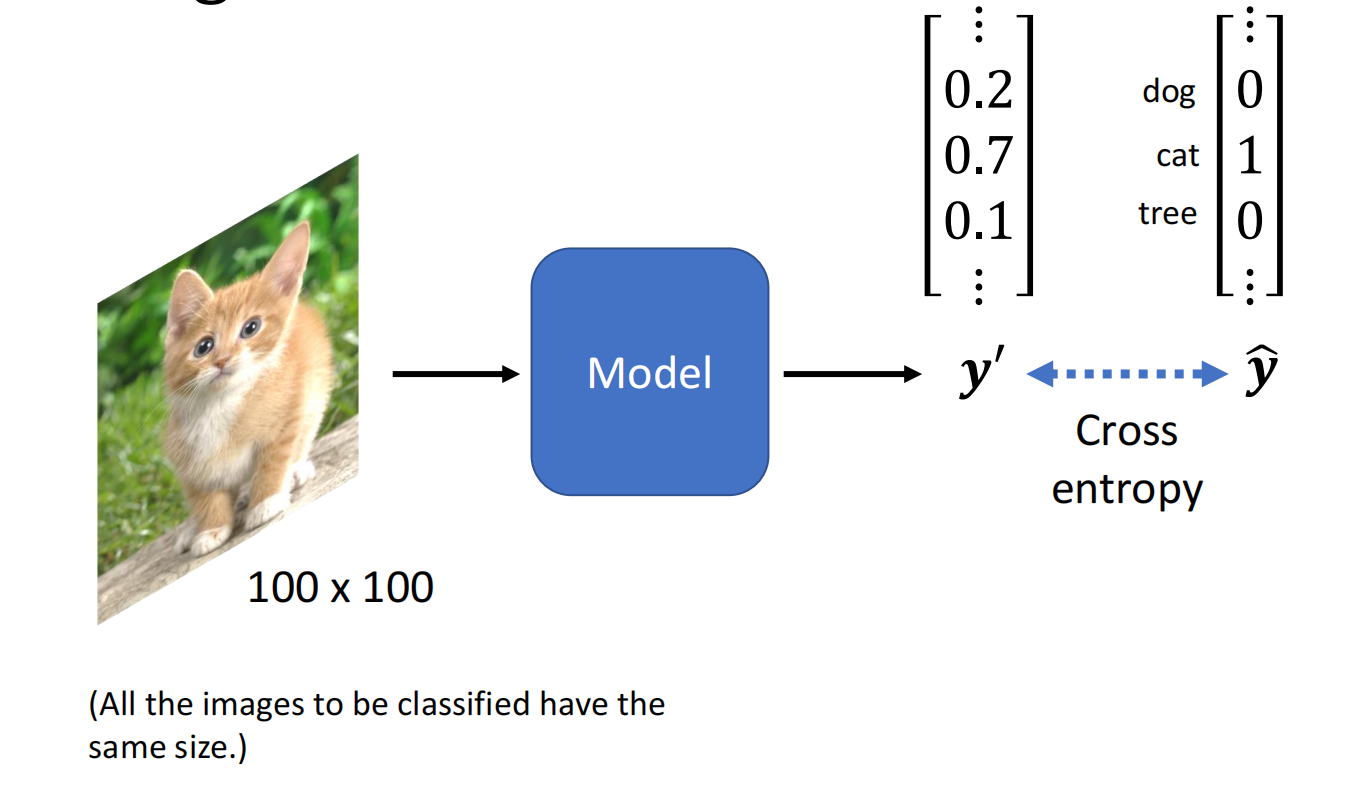
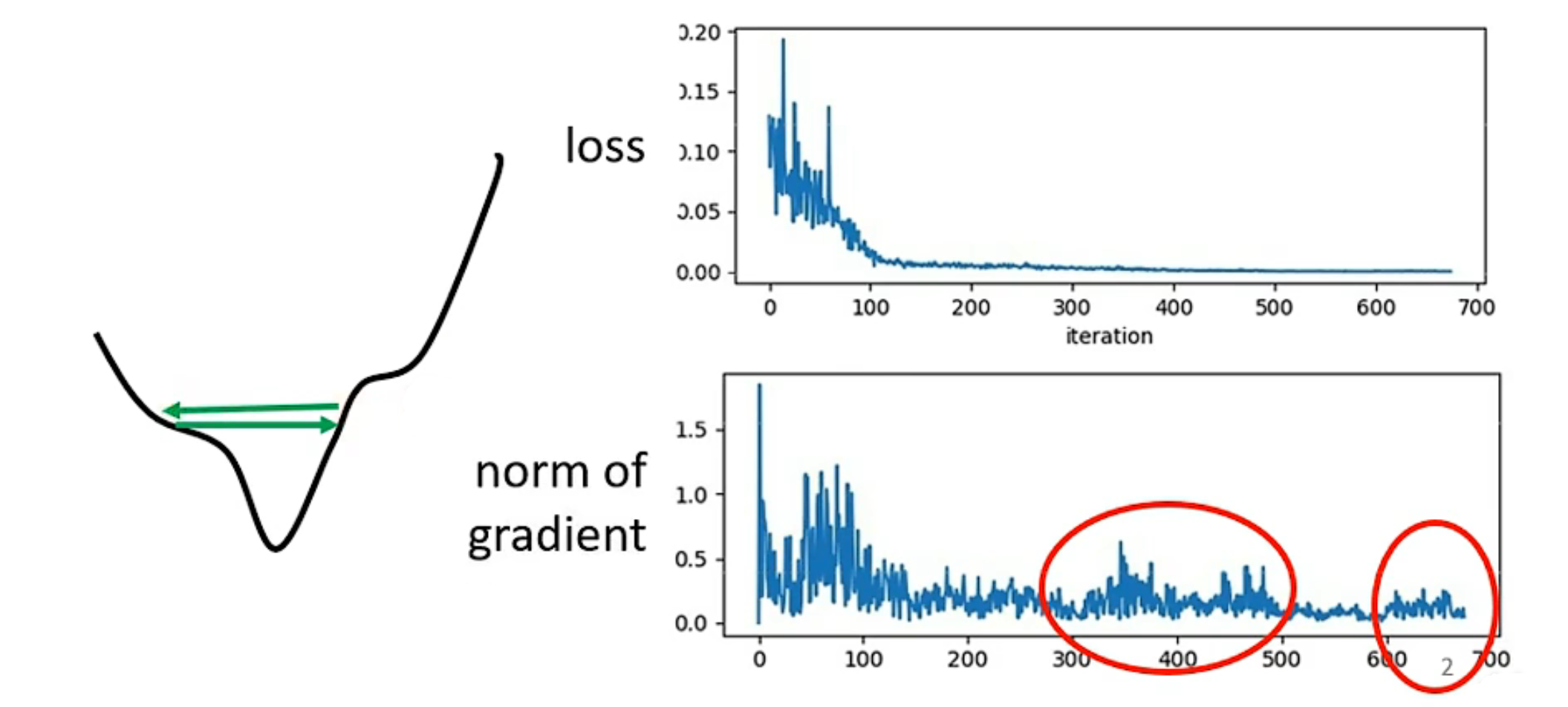
Machine Learning

机器学习就是让机器具备找一个函式的能力。

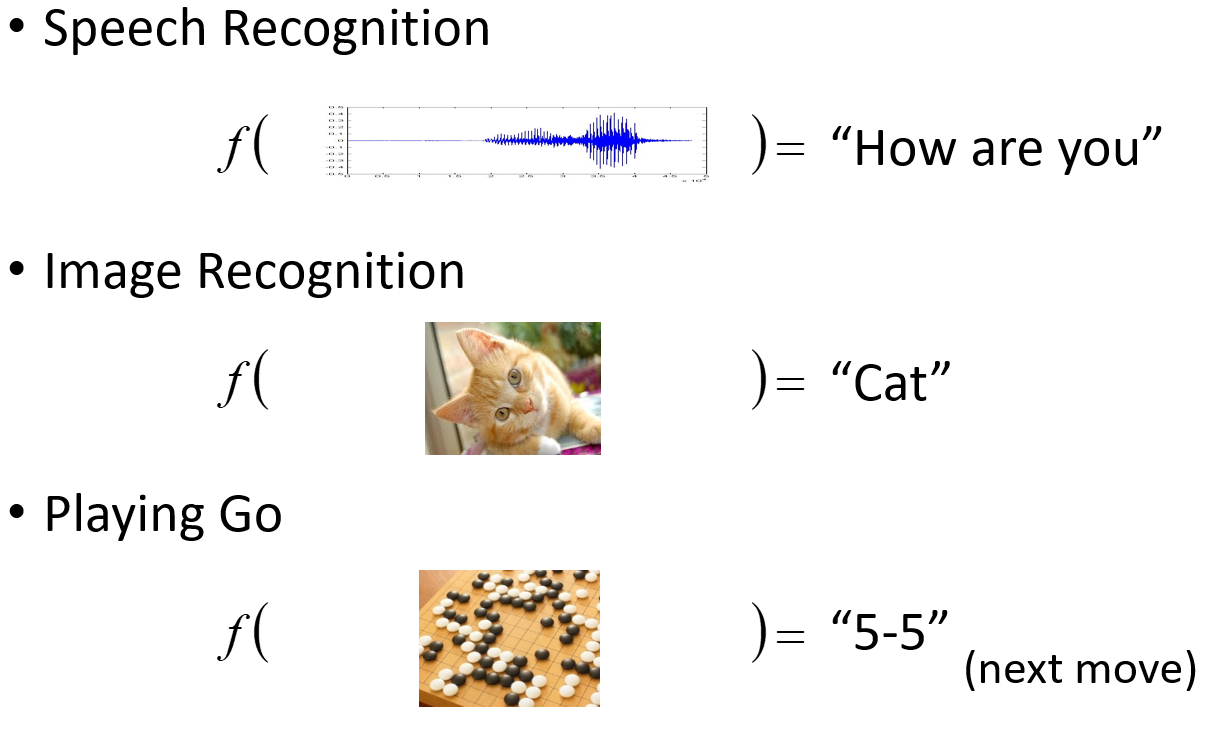
image-20210918143931046

我们期待凭借着机器的力量,把这个函式自动找出来，这件事情，就是机器学习。

Different types of Functions

  • Regression（回归）: The function outputs a scalar.

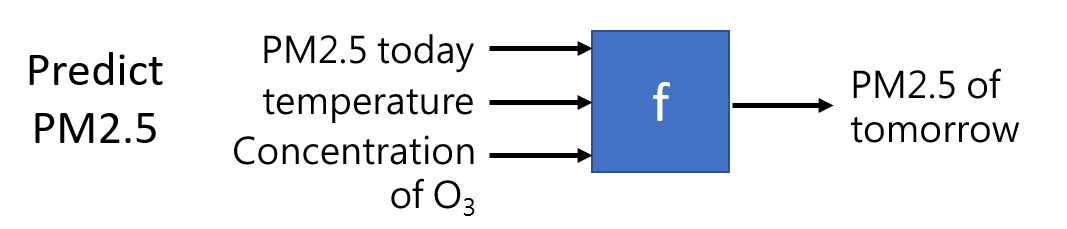
image-20210918144110296

找这个函数f的任务，称之为Regression

  • Classification（聚类）: Given options (classes), the function outputs the correct one.

从设定好的选项里面选择一个当作输出，这个任务就叫作Classification

image-20210918144406145

例如，设定输出结果为Yes和No两个选项

  • Structured Learning：让机器产生有结构的东西，例如：画一张图。

机器学习训练的步骤

  1. 构造一个带有未知参数的函数（Function with Unknown Parameters）

先猜测一下我们打算找的函数$f$，他的数学表达式是什么

image-20210918145425523

  1. 定义一个Loss（Define Loss from Training Data）

Loss是一个Function，输入是模型里的参数：$L(b, w)$，描述一个vlaue的好坏

  1. 最佳化问题(Optimization)

找到一组 $w, b$ 使得 $w^*, b^* = arg \min_{w,b} L$

（1） 先来看只有一种参数的情况，假设目前 $b$ 是确定的

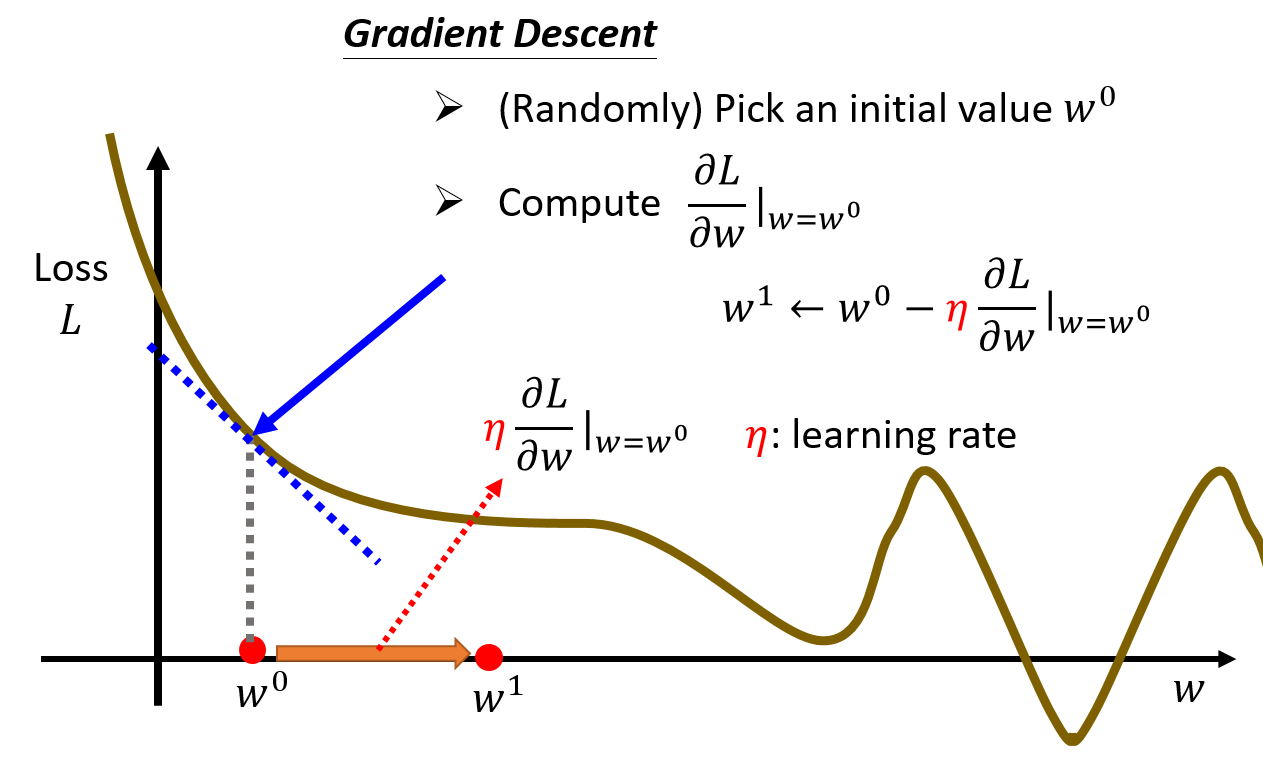
image-20211007202730339

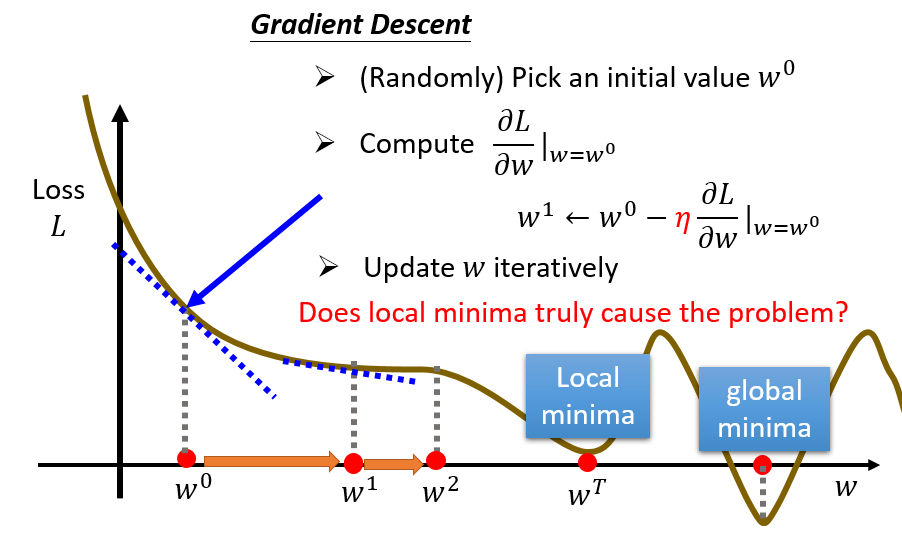
image-20211007203141620

（2） 再来看两种参数的情况

  • 随机设定一个 $w^0, b^0$ 初始点
  • 计算
    • $\frac{\partial L}{\partial w}|w=w^0, b=b^0$, $w^1←w^0-η\frac{\partial L}{\partial w}|w=w^0, b=b^0$
    • $\frac{\partial L}{\partial b}|w=w^0, b=b^0 $, $b^1←b^0-η\frac{\partial L}{\partial b}|w=w^0, b=b^0 $
  • 一直更新 $w$ 和 $b$，直到Loss最小

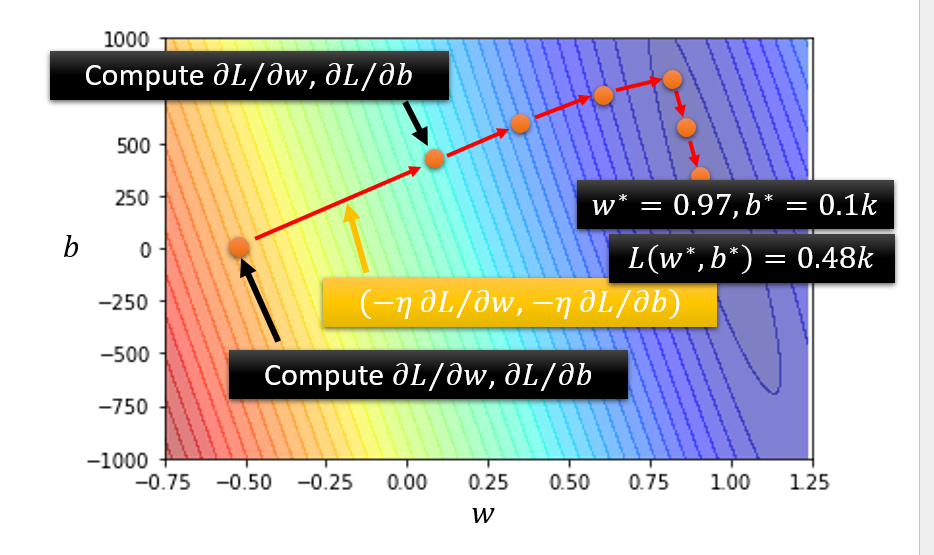
image-20211007204511502

Model Bias：线性模型过于简单，很多时候不能准确的预测结果，因此我们需要一个更复杂的模型

All Piecewise Linear Curves = 初始值 + 一堆function的集合

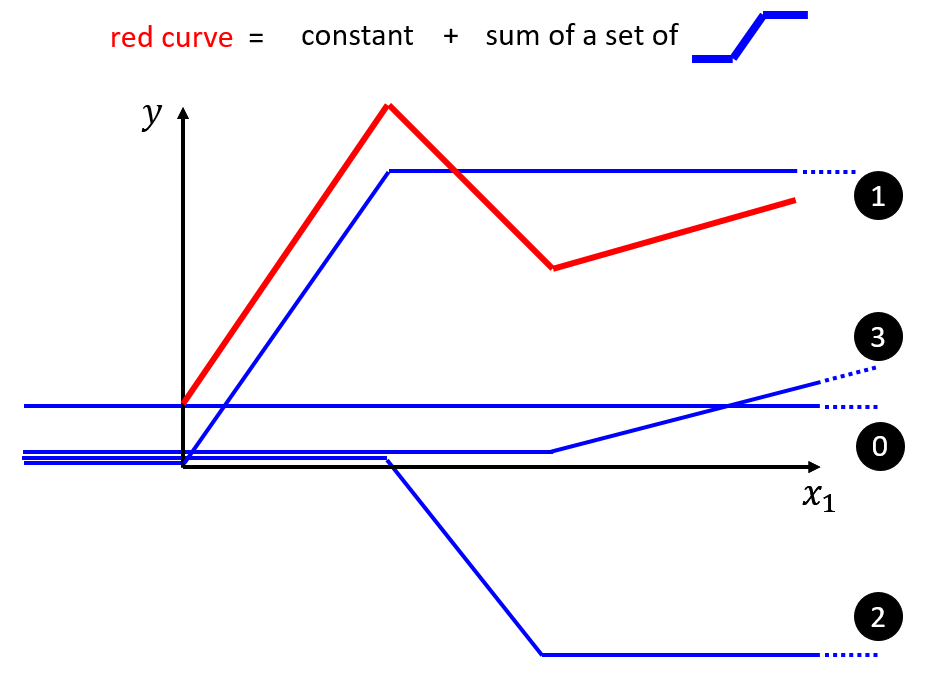
image-20211007211529936

如果是曲线，那么曲线上的点取得越多，结果就越逼近曲线

构造function（S型函数）：

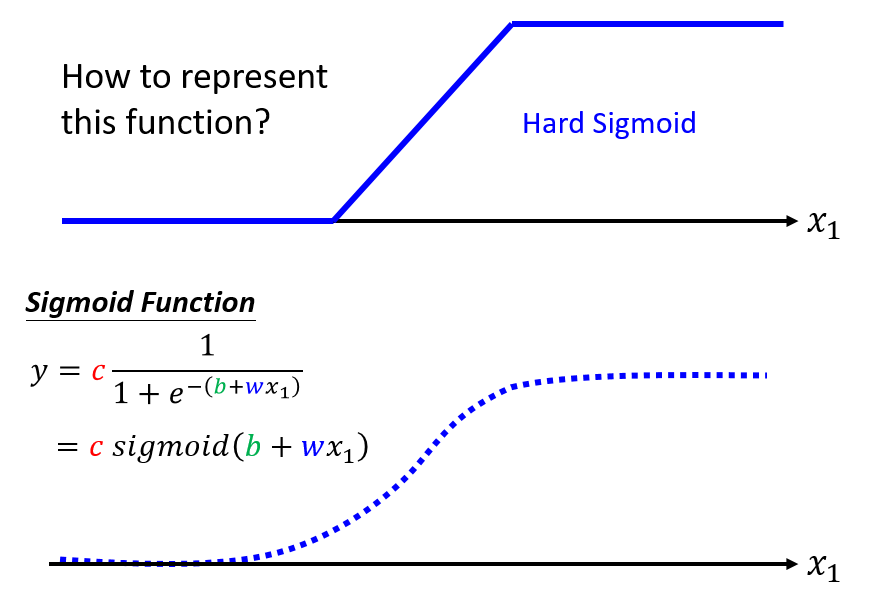
image-20211007211301572

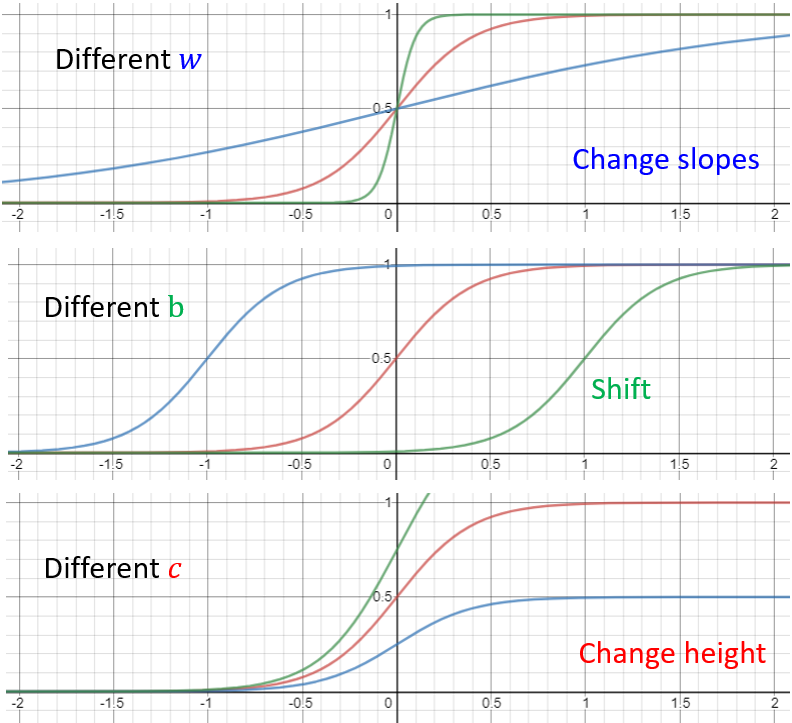
通过调整 $c, b, w$，可以得到各种sigmoid function去逼近Hard Sigmoid(激活函数的一种)

image-20211007211434978

对于red curve， $y = b + \sum_{i} c_{i} sigmoid(b_{i}+w_{i}x_{1})$

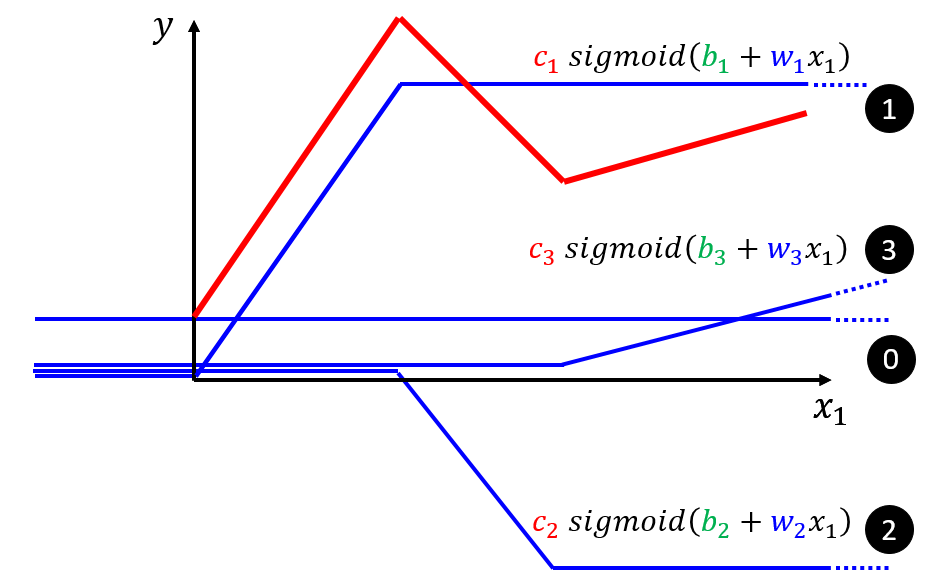
image-20211007211752606

如果 $b, w, c$ 是未知的参数，我们就可以设定不同的 $b, w, v$，制造出不同的red curve

$y = b + wx_{i}$

$ \to y = b + \sum_{i} c_{i} \cdot sigmoid(b_{i}+w_{i}x_{1})$

$y = b + \sum_{j}w_{j}x_{j}$

$\to y = b + \sum_{i} c_{i} \cdot sigmoid(b_{i} + \sum_{j} w_{ij}x_{j})$

image-20211007214834123

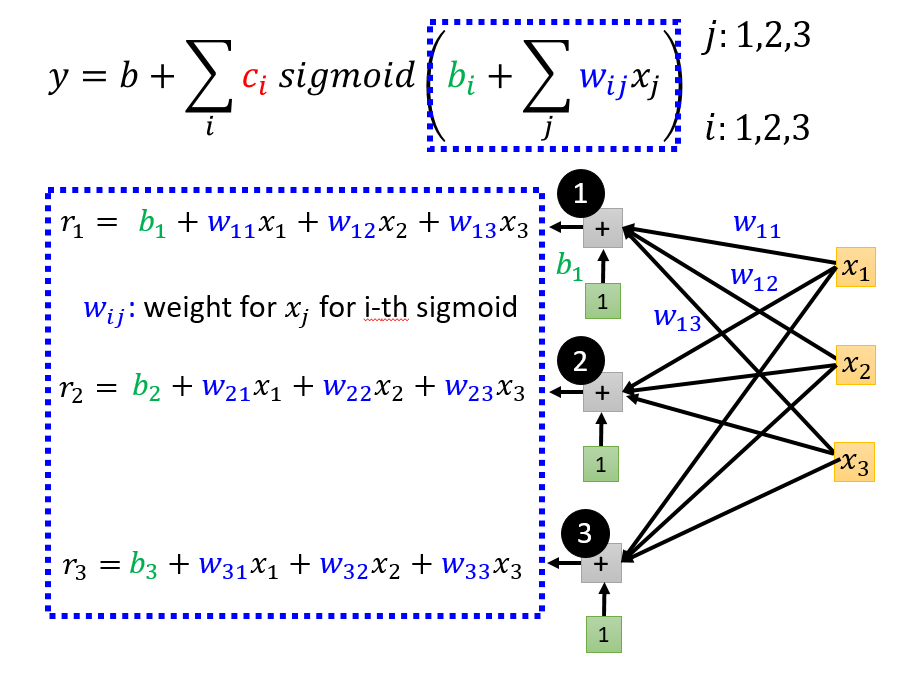
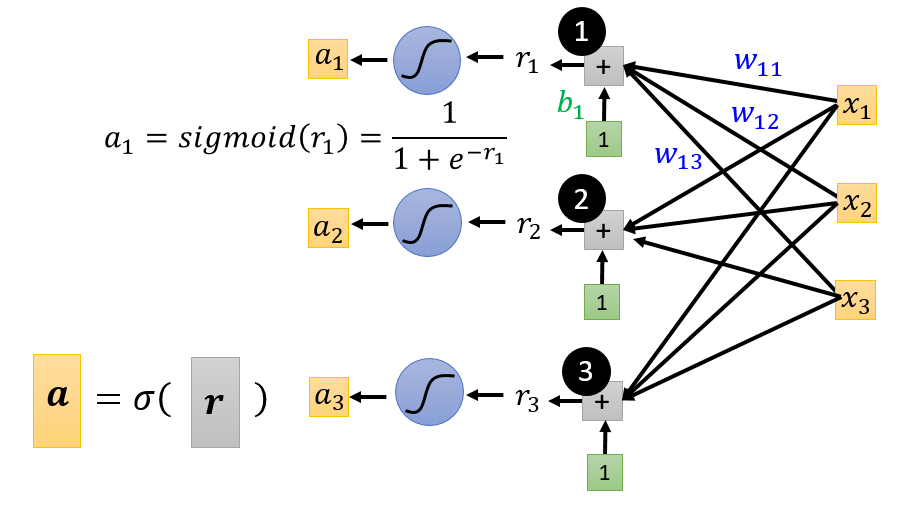
image-20211007215531464

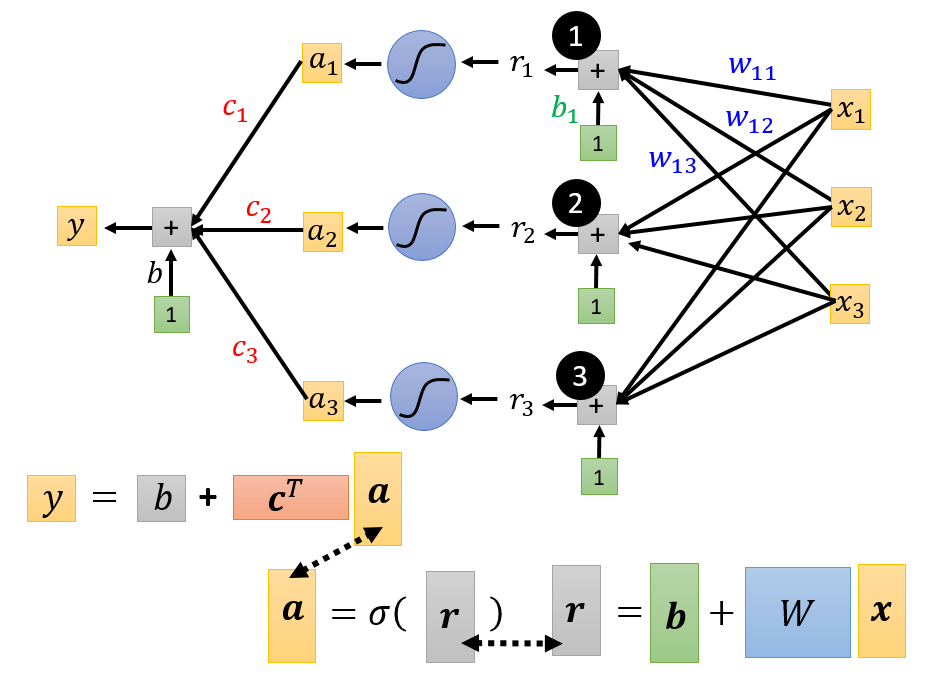
image-20211007215549801

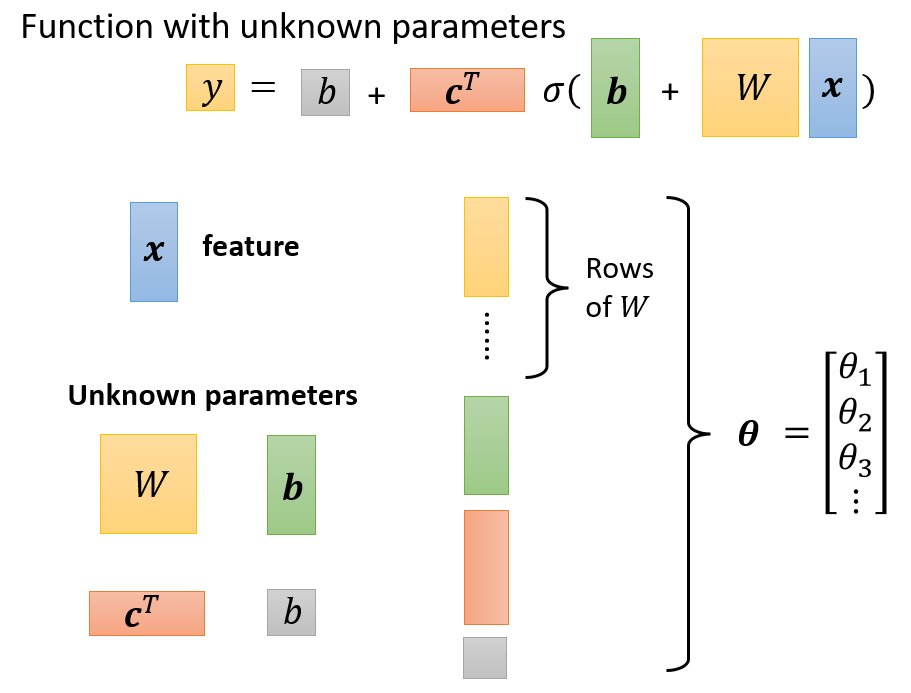
image-20211007215744001

此时，我们重新回到原来的三个步骤

  1. 构造未知表达式：$y = b + c^T \cdot \sigma (b+Wx)$

  2. 定义Loss

    1. Loss是函数的一个参数：$L(\theta)$
    2. Loss表明一组值的集合的好坏
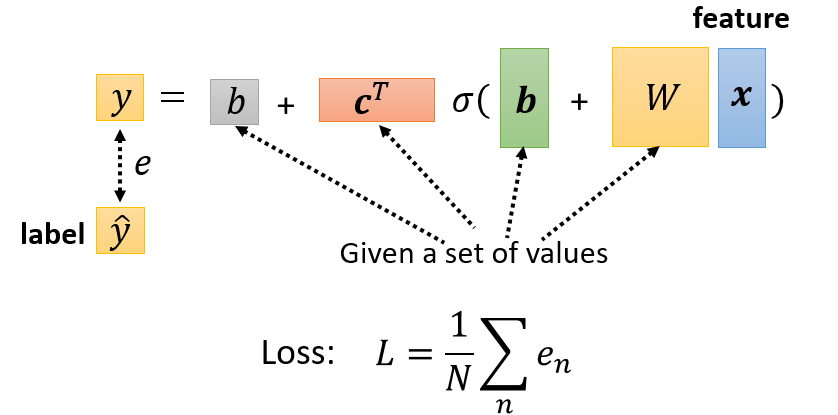
    3. image-20211007222441861

  3. 最优化（optimization）

image-20211007222704509

随机选一个初始的 $\theta^0$，对每一个未知的参数 $\theta_{i}$ 去计算对 $L$ 的微分，集合起来就是一个向量，用 $g$ 表示，称为gradient（梯度）

$g = \bigtriangledown L(\theta^0)$

然后更新参数，直到停止（停止条件：设置次数或者结果为0）

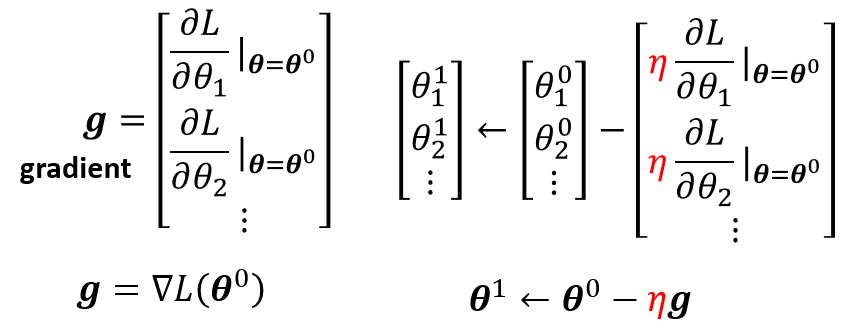
image-20211007222851339

通常来说，我们会这么做

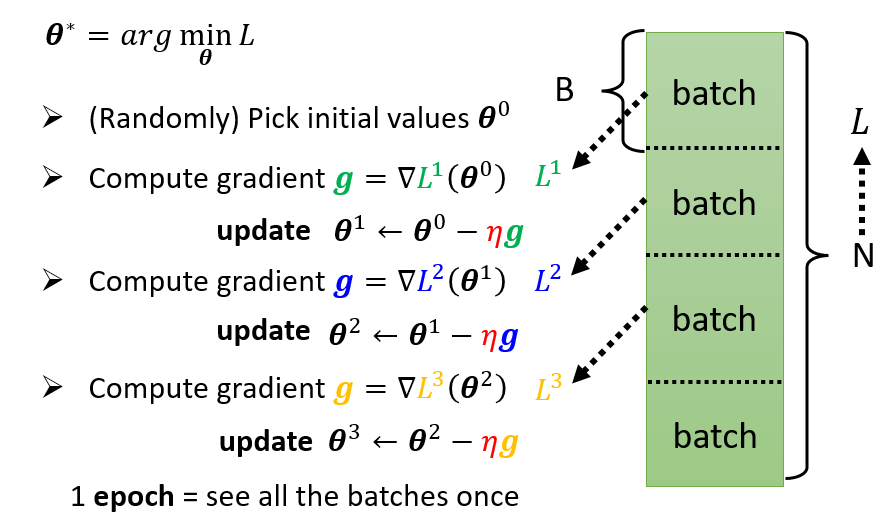
image-20211007223529334

  • 把所有batch都看过一次，称之为一个epoch
  • 每一次更新参数都叫做一次update

例如：10,000 examples (N = 10,000)、Batch size is 10 (B = 10)，一次epoch中有1000次update

其实我们还可以对模型做出更多的变形

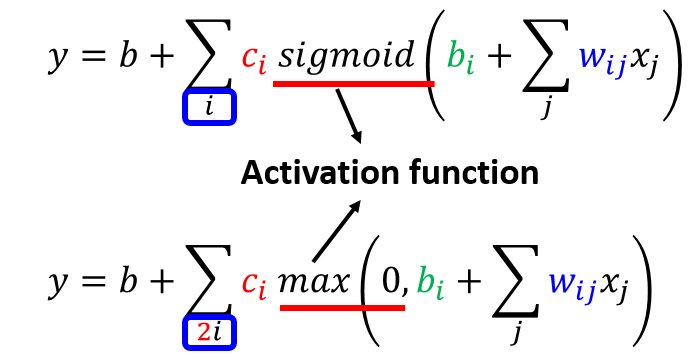
  1. ReLU

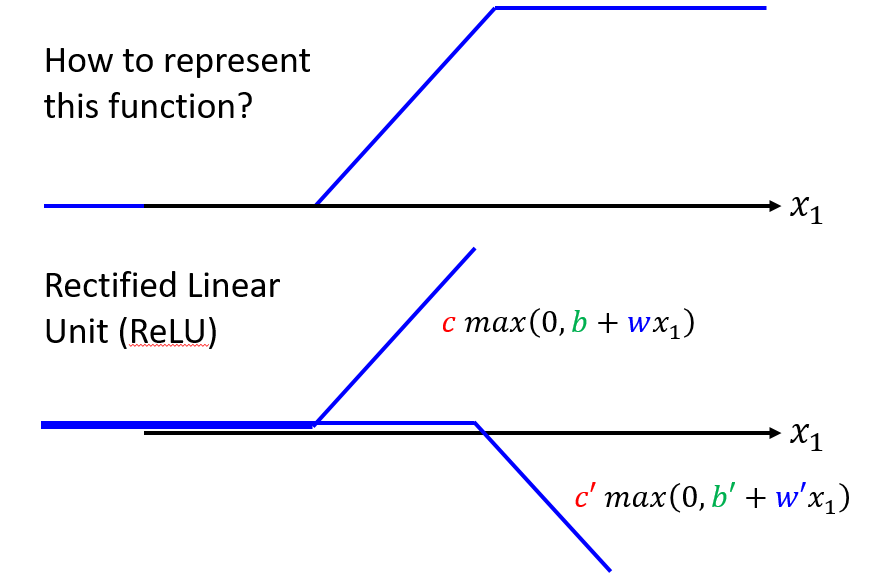
image-20211007224121935

可以把Hard Sigmoid看作两个ReLU（Rectified Linear Unit）的加总。

这些都是激活函数（Activation Function）

image-20211007224354750

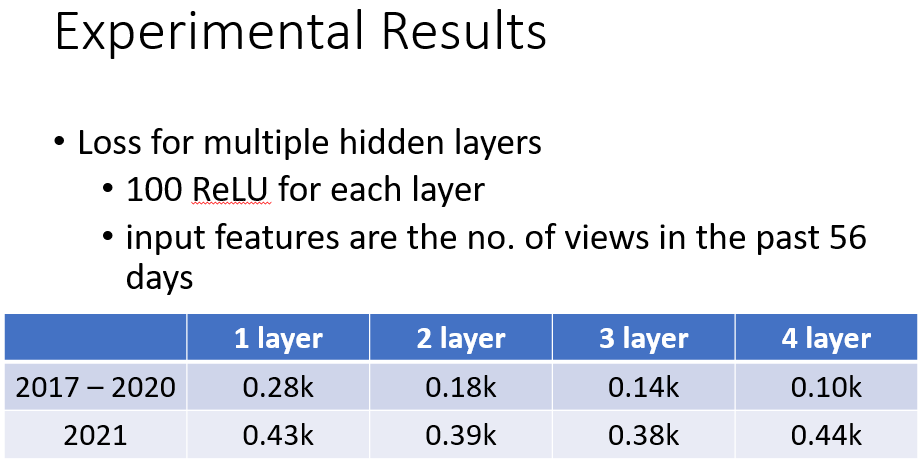
image-20211007224940087

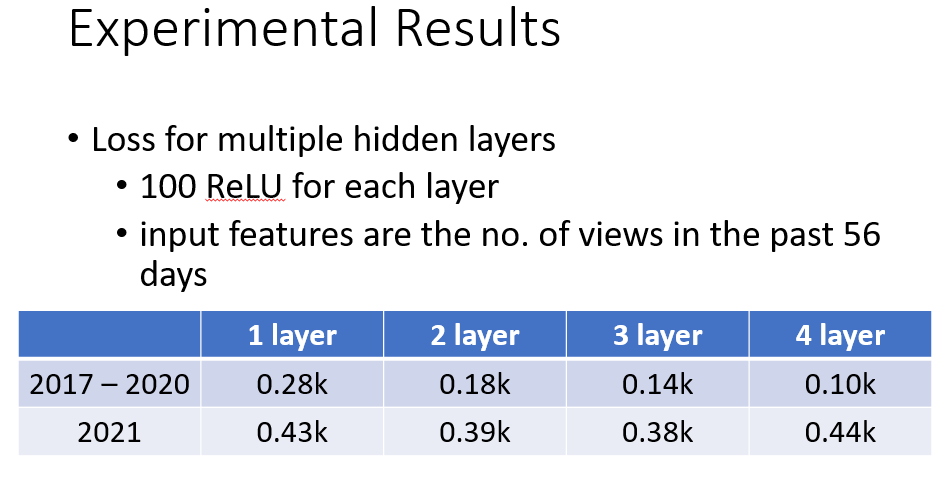
  1. Layer（增加层数）

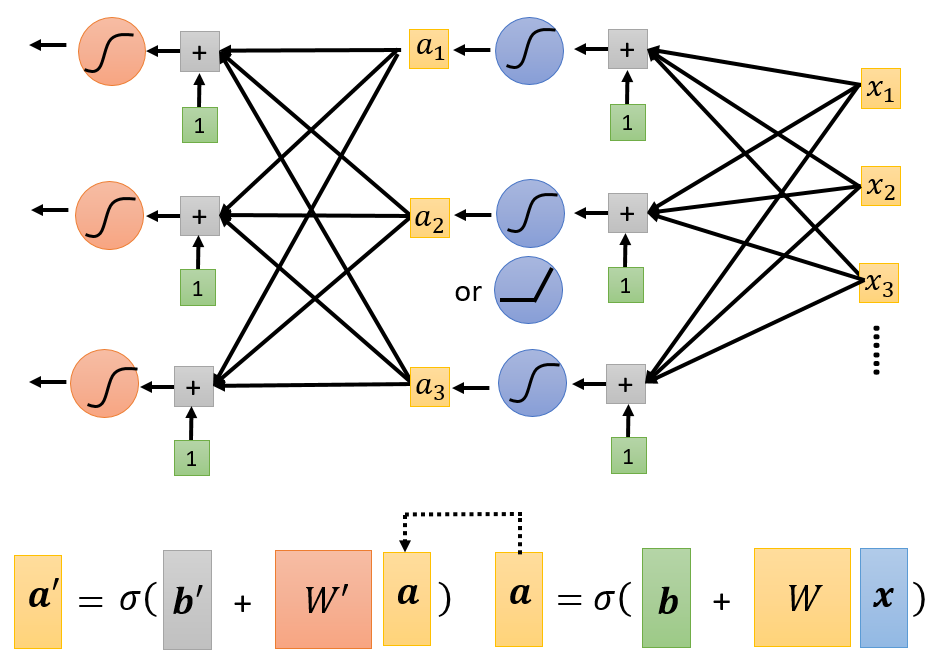
image-20211007224905262

image-20211007224926998

这些Sigmoid或ReLU，被称为Neuron（神经元），很多Neuron被称为Neuron Network（这玩意现在写paper会被拒）

所以新的名字：

  • 每一排Neural叫做一个Layer，他们叫Hidden Layer
  • 很多的Hidden Layer就叫做Deep
  • 整套技术就叫做Deep Learning