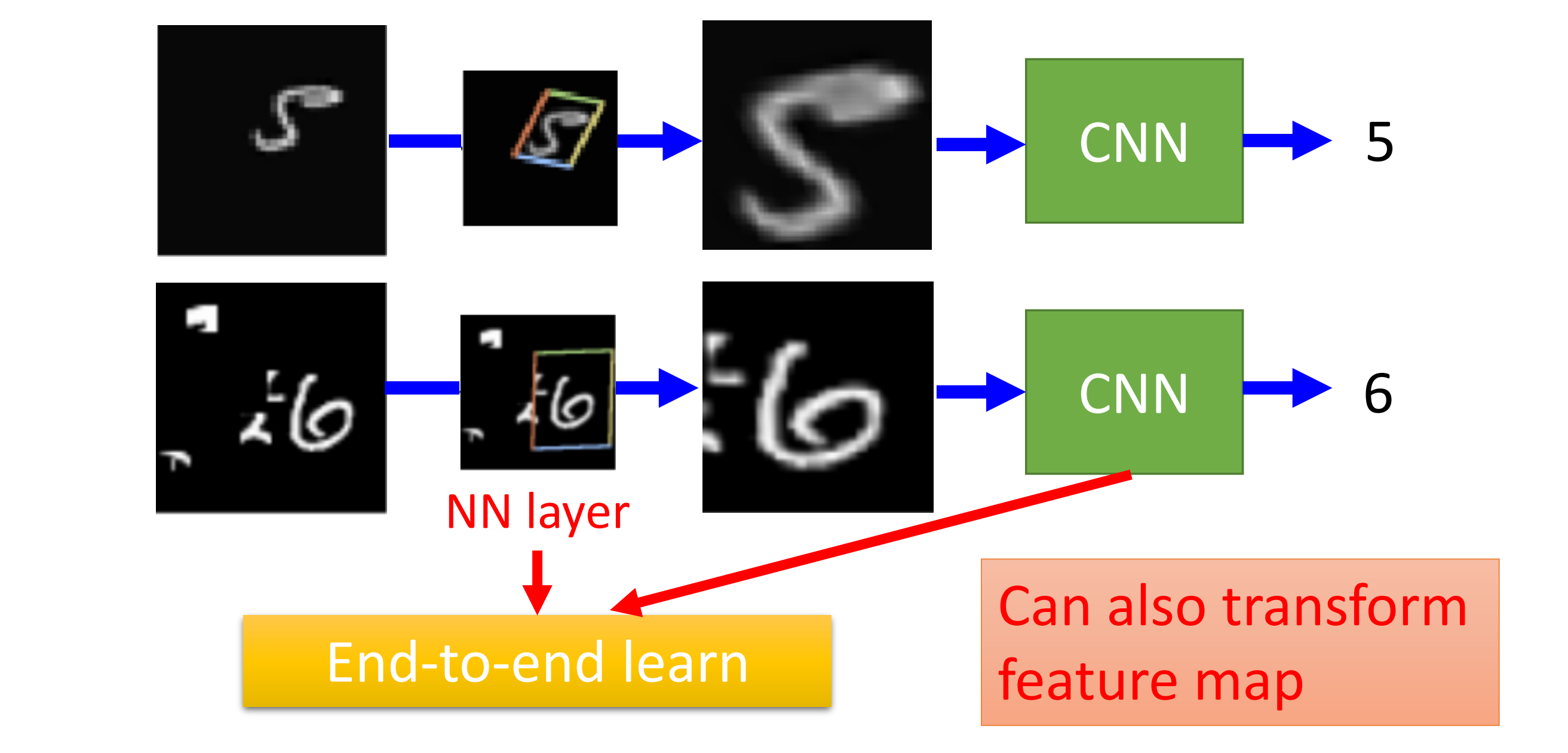
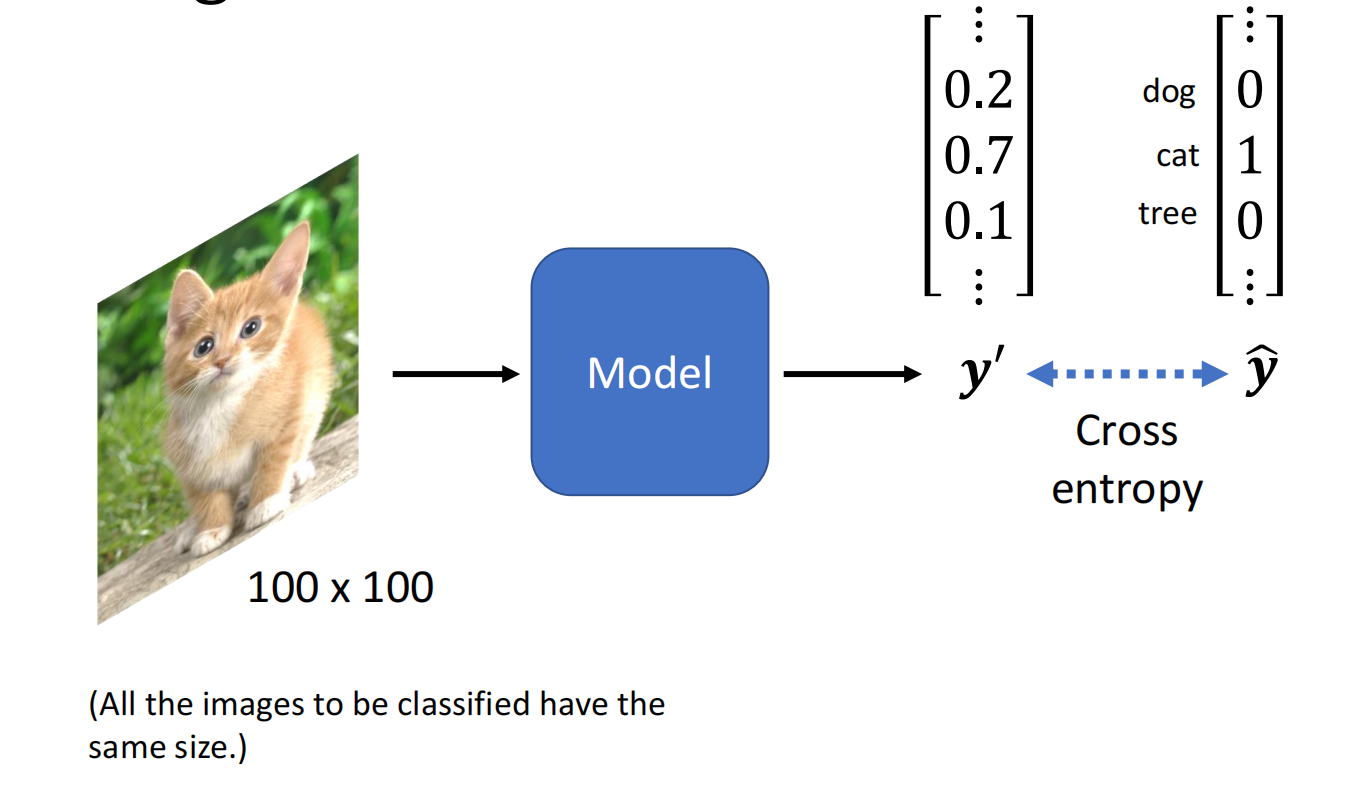
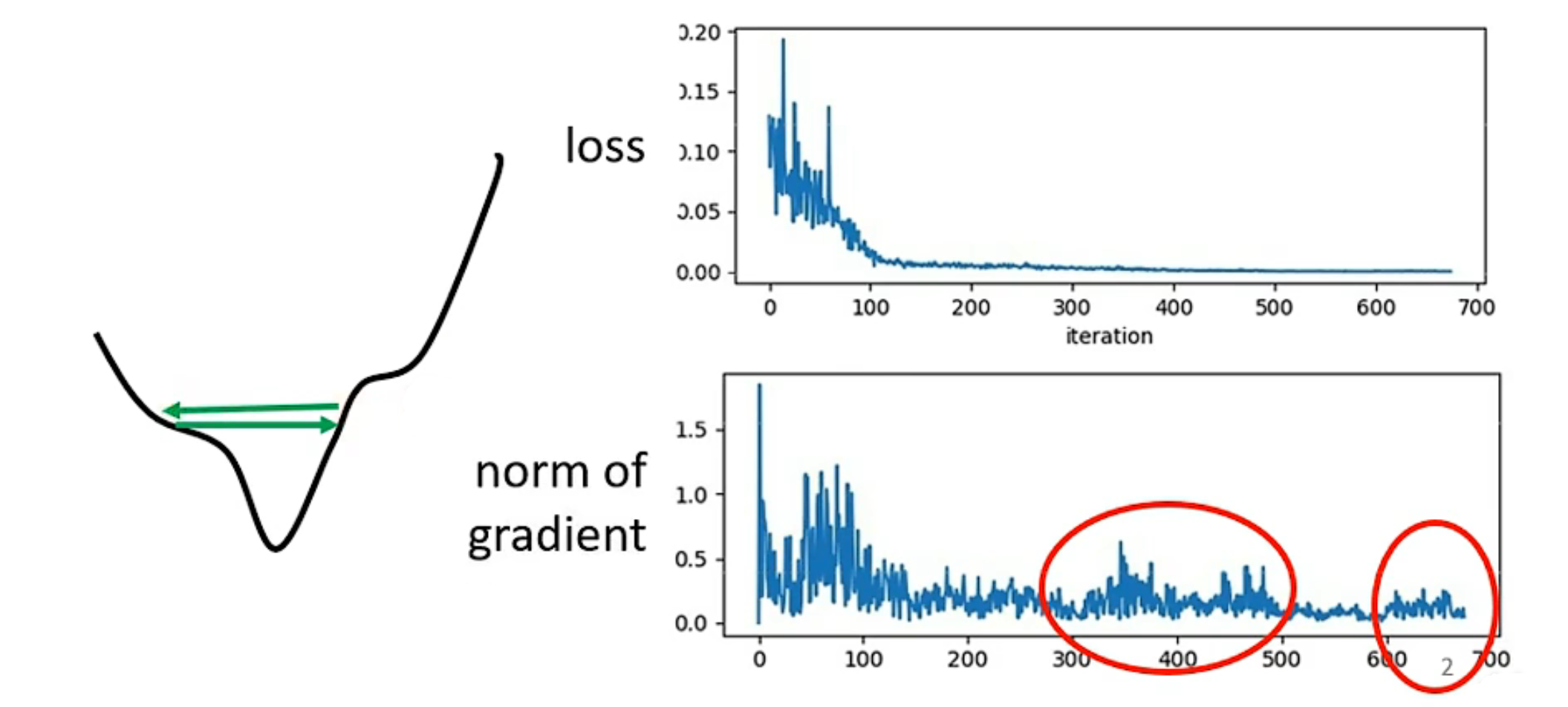
逻辑回归

1. Function Set

以下依旧假设是二元分类，根据上节的计算我们得出我们的Model是一个关于 $z$ 的函数 $δ(z)$.

将其图形化：

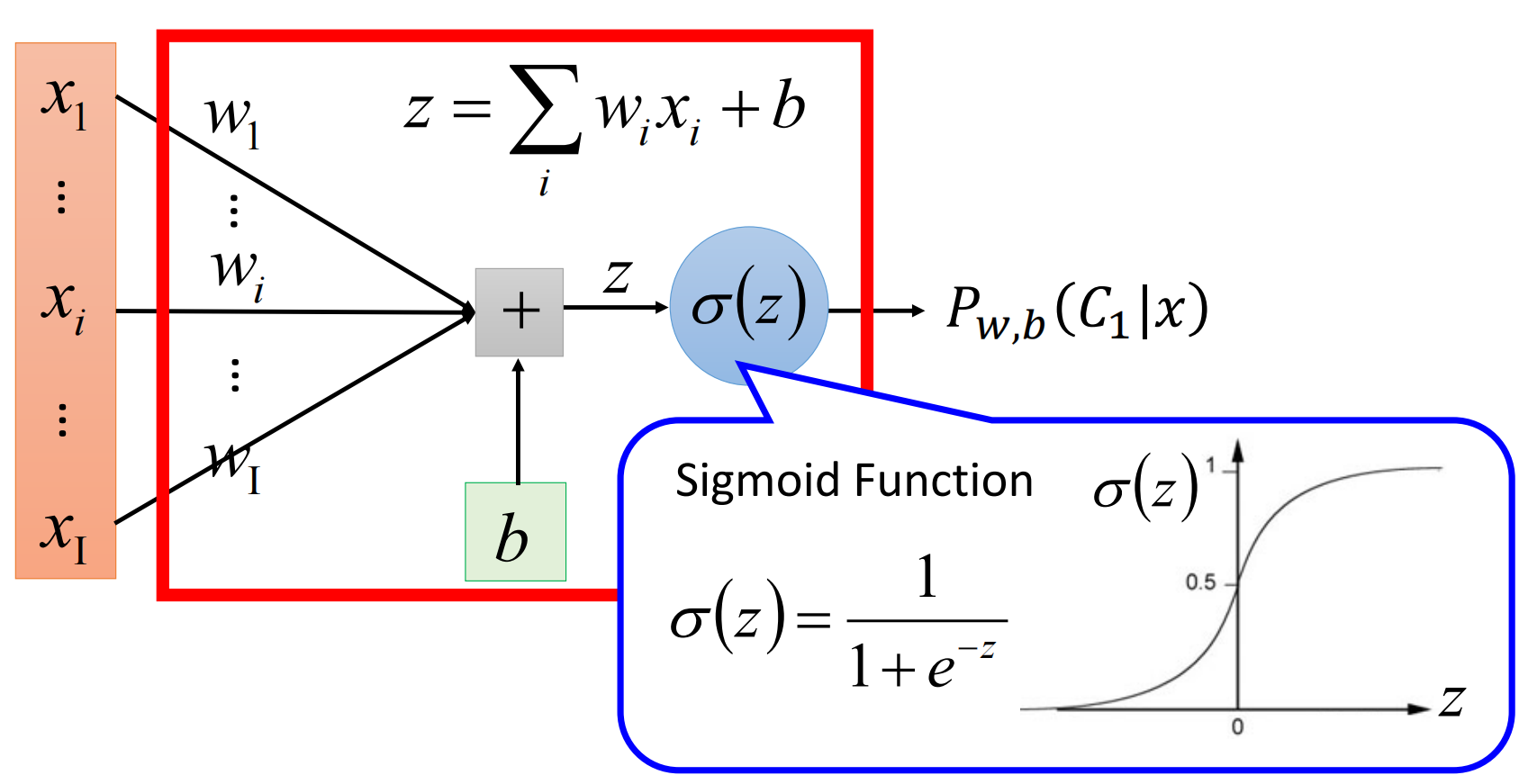
2. Goodness of a Function

假设数据是根据 $f_{w, b}(x)=P_{w, b}\left(C_{1} \mid x\right)$ 产生的
根据某一特定的 $w$ 和 $b$，产生数据的概率：
$L(w, b)=f_{w, b}\left(x^{1}\right) f_{w, b}\left(x^{2}\right)\left(1-f_{w, b}\left(x^{3}\right)\right) \cdots f_{w, b}\left(x^{N}\right)$

最好（最大几率产生数据集）的 $w^{*}$ 和 $b^*$ ：$w^{*}, b^{*}=\arg \max _{w, b} L(w, b)$

3. Find the best function

使用梯度下降即可，以下为数学公式的推导

逻辑回归与线性回归

第一步中：

• 逻辑回归的输出一定是介于0-1之间
• 线性回归的输出可以为任何值

第二步中：

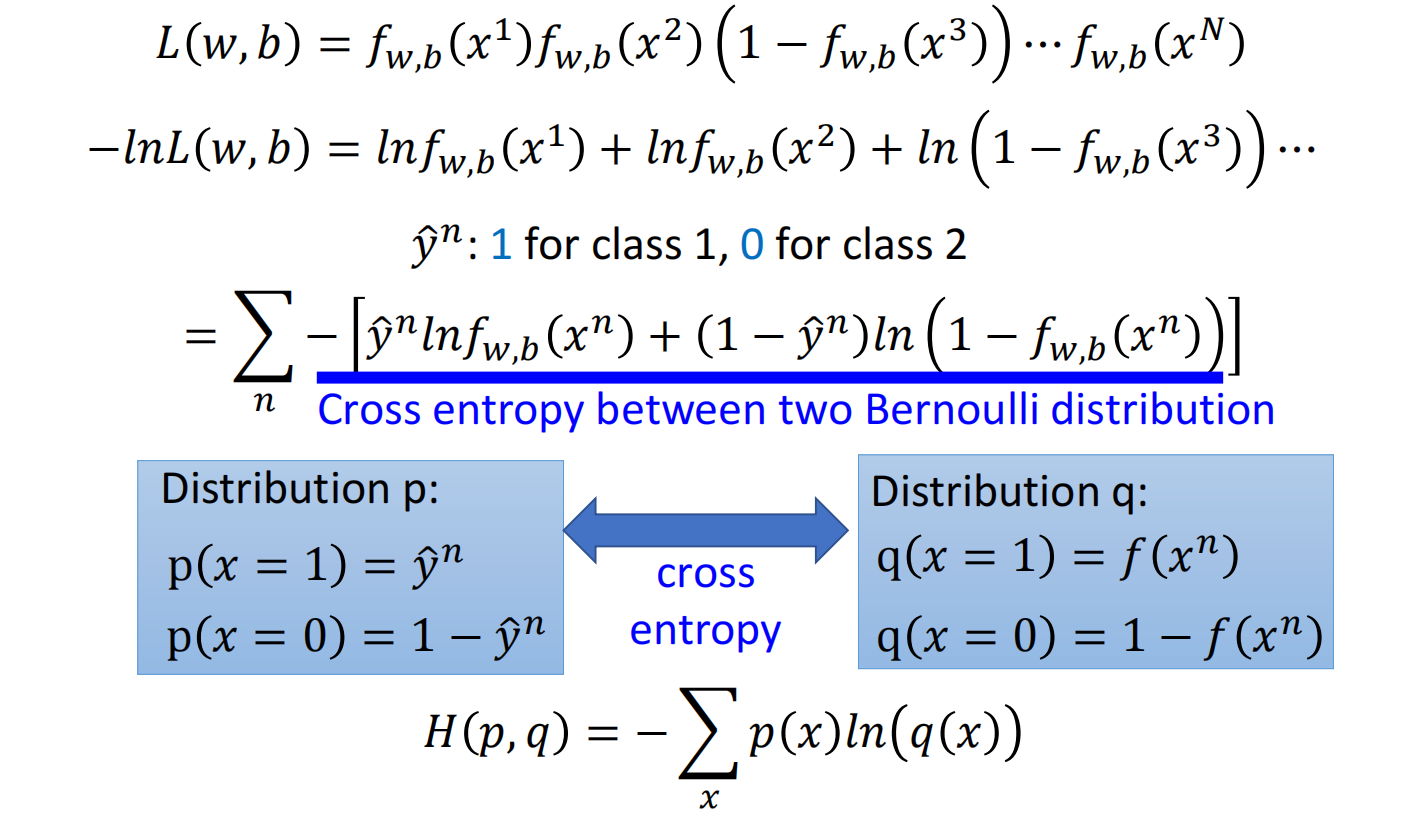
• 对于逻辑回归，交叉熵：$l\left(f\left(x^{n}\right), \hat{y}^{n}\right)=-\left[\hat{y}^{n} \ln f\left(x^{n}\right)+\left(1-\hat{y}^{n}\right) \ln \left(1-f\left(x^{n}\right)\right)\right]$
• 对于线性回归，略

第三步中：

• 二者梯度下降的公式是基本一样的，只有target范围不一致

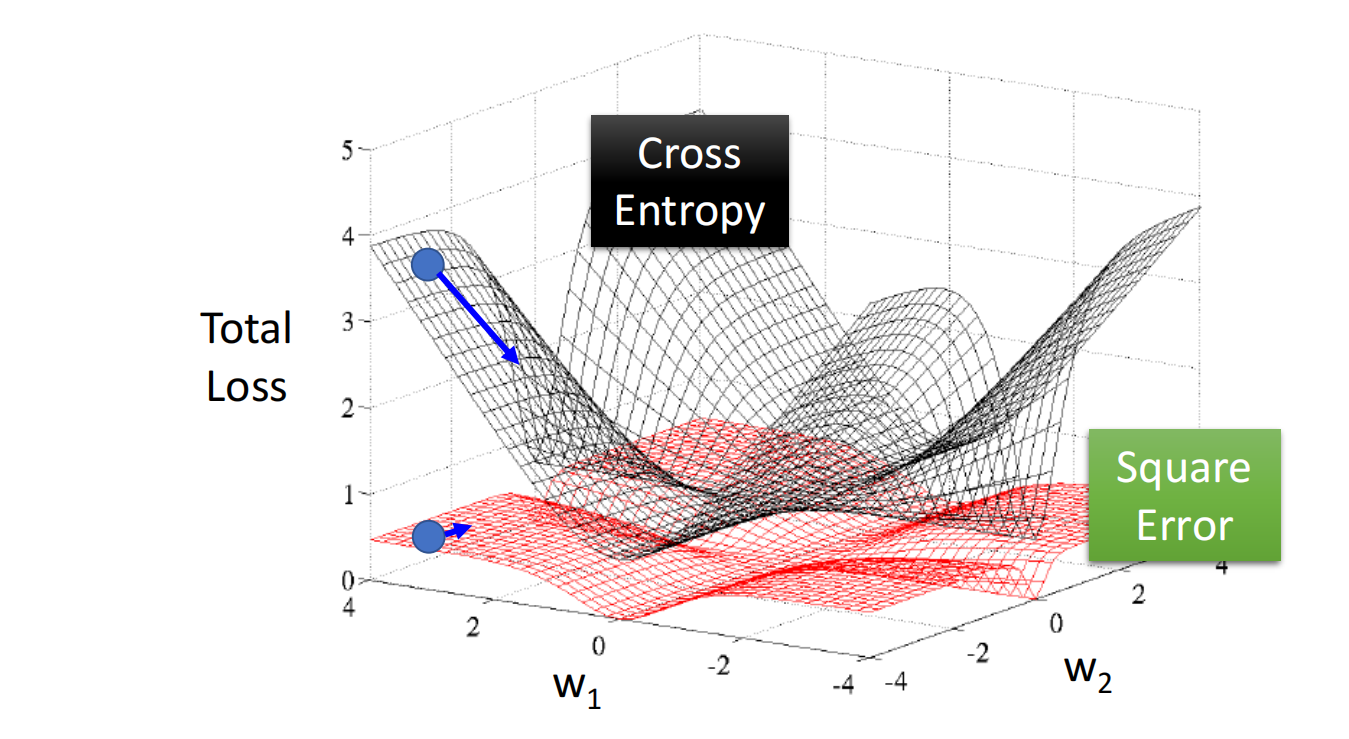
逻辑回归不能用均方差损失函数

如果使用逻辑回归模型，但在第二步时省事使用平方差损失函数，而不是使用交叉熵损失函数的话

当 $f(x)=1$（接近目标） 或 $f (x)=0$（离目标很远） 时，微分结果为0，导致梯度下降更新参数很慢

线性回归没有sigmoid函数映射，不会造成此问题

逻辑回归的局限性

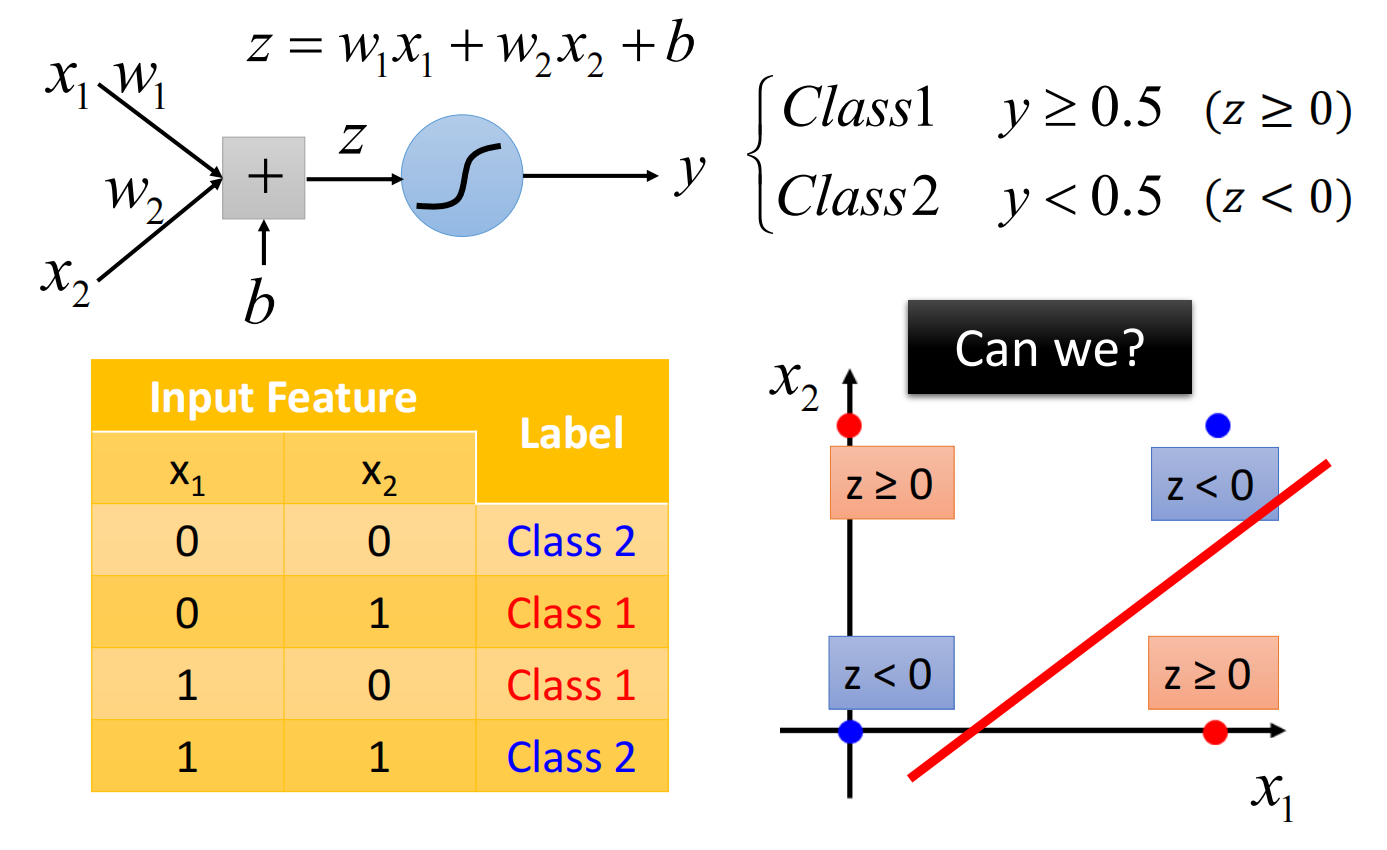
逻辑回归是线性的，无法解决这个问题

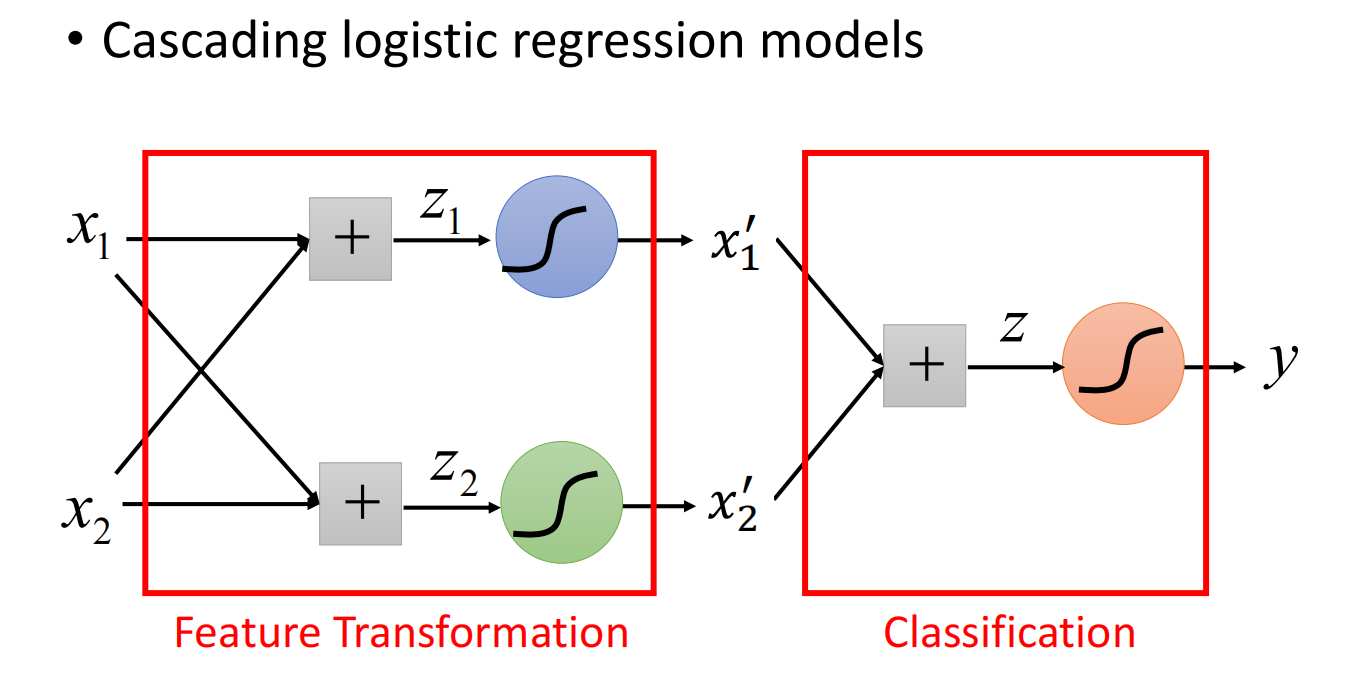
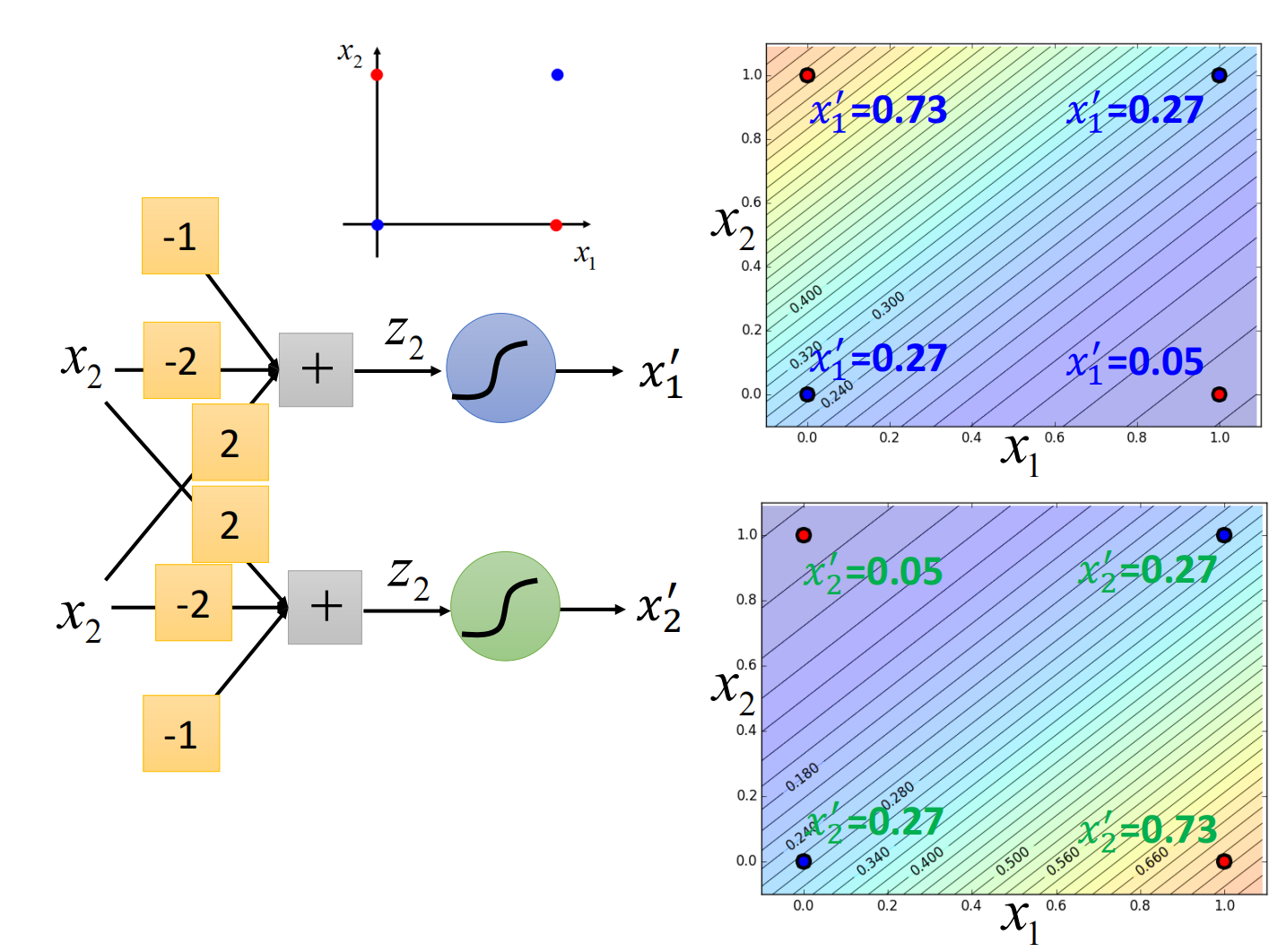
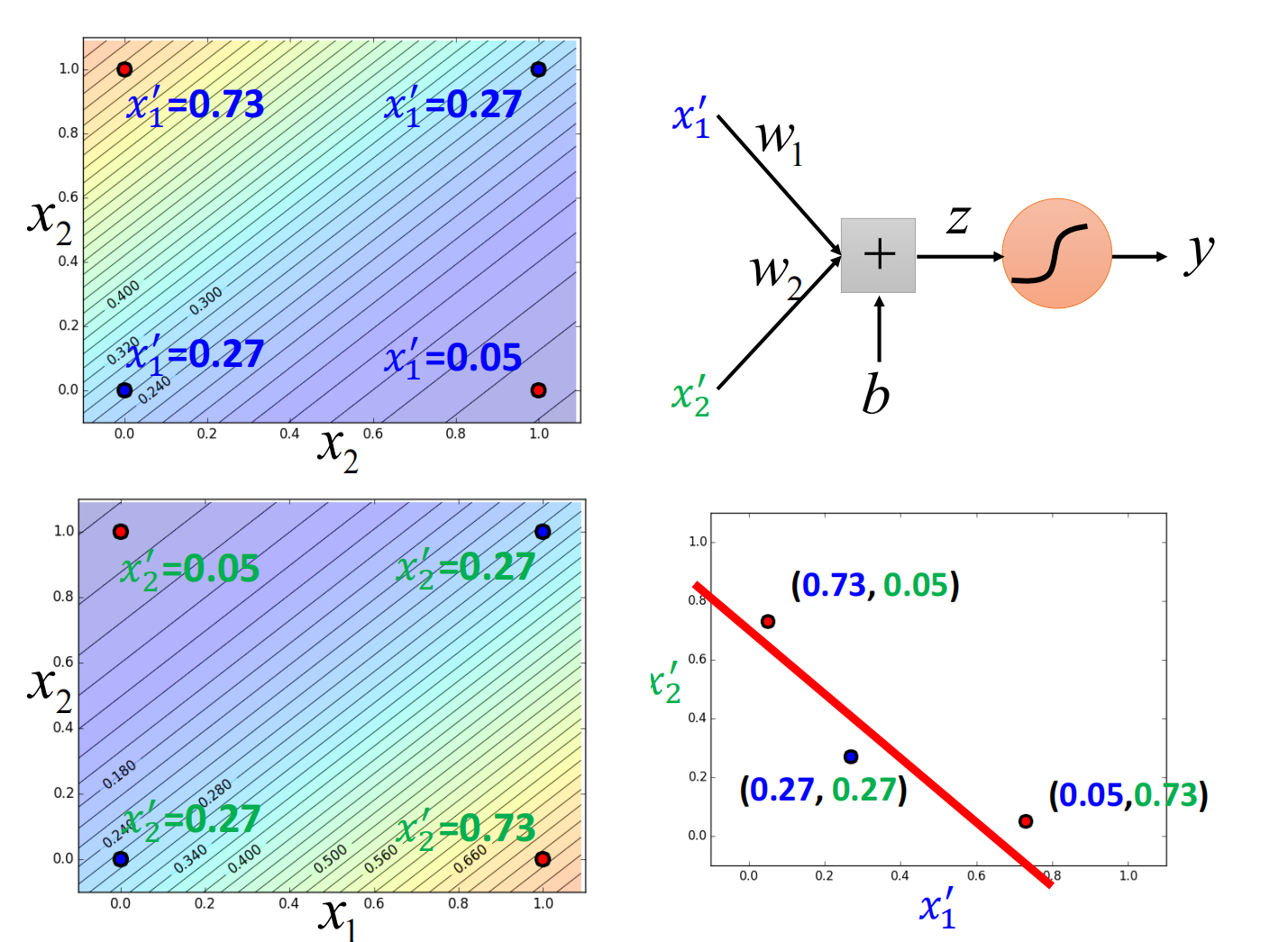
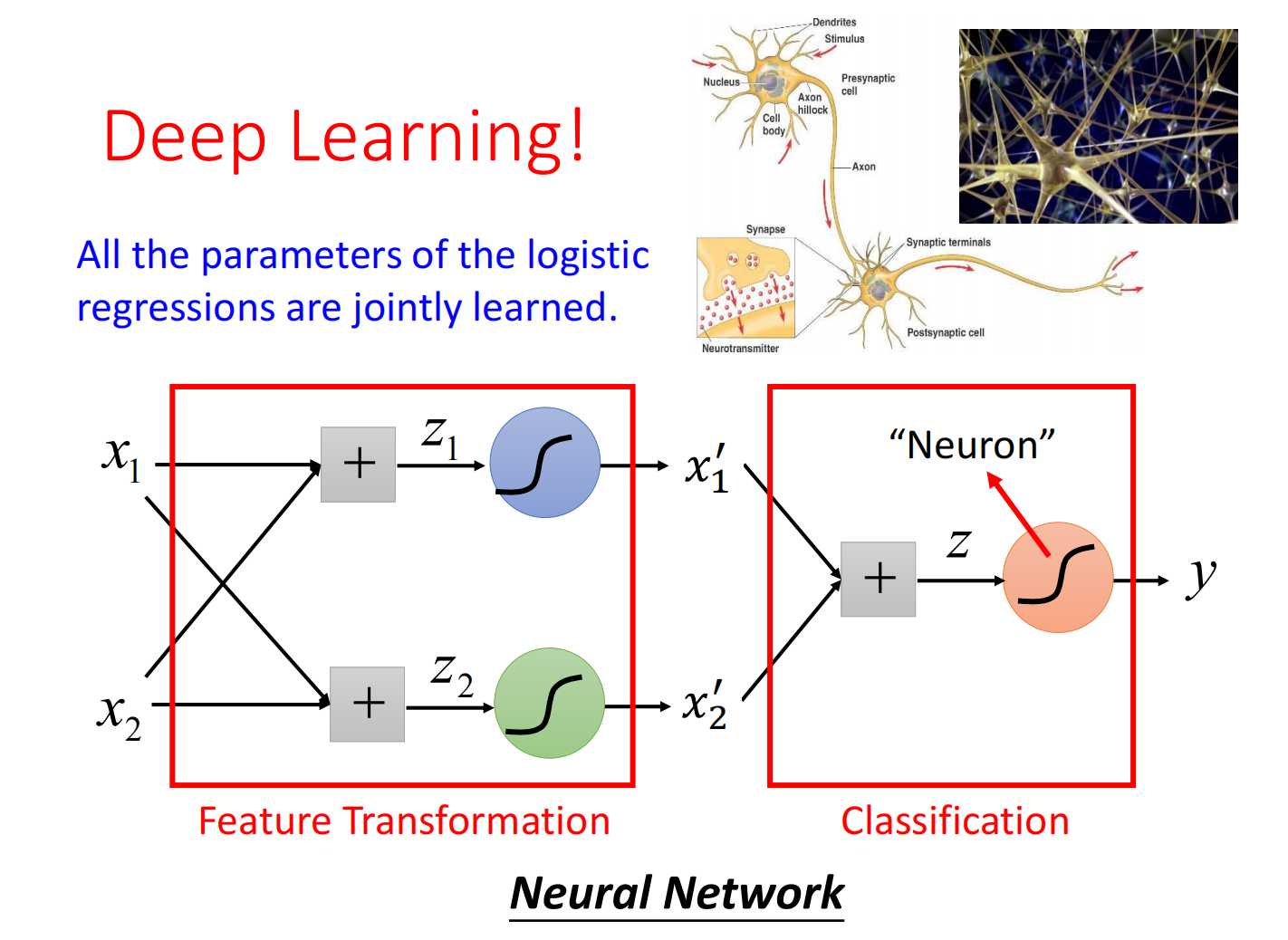
但我们可以是使用特征变换（Feature Transformation）

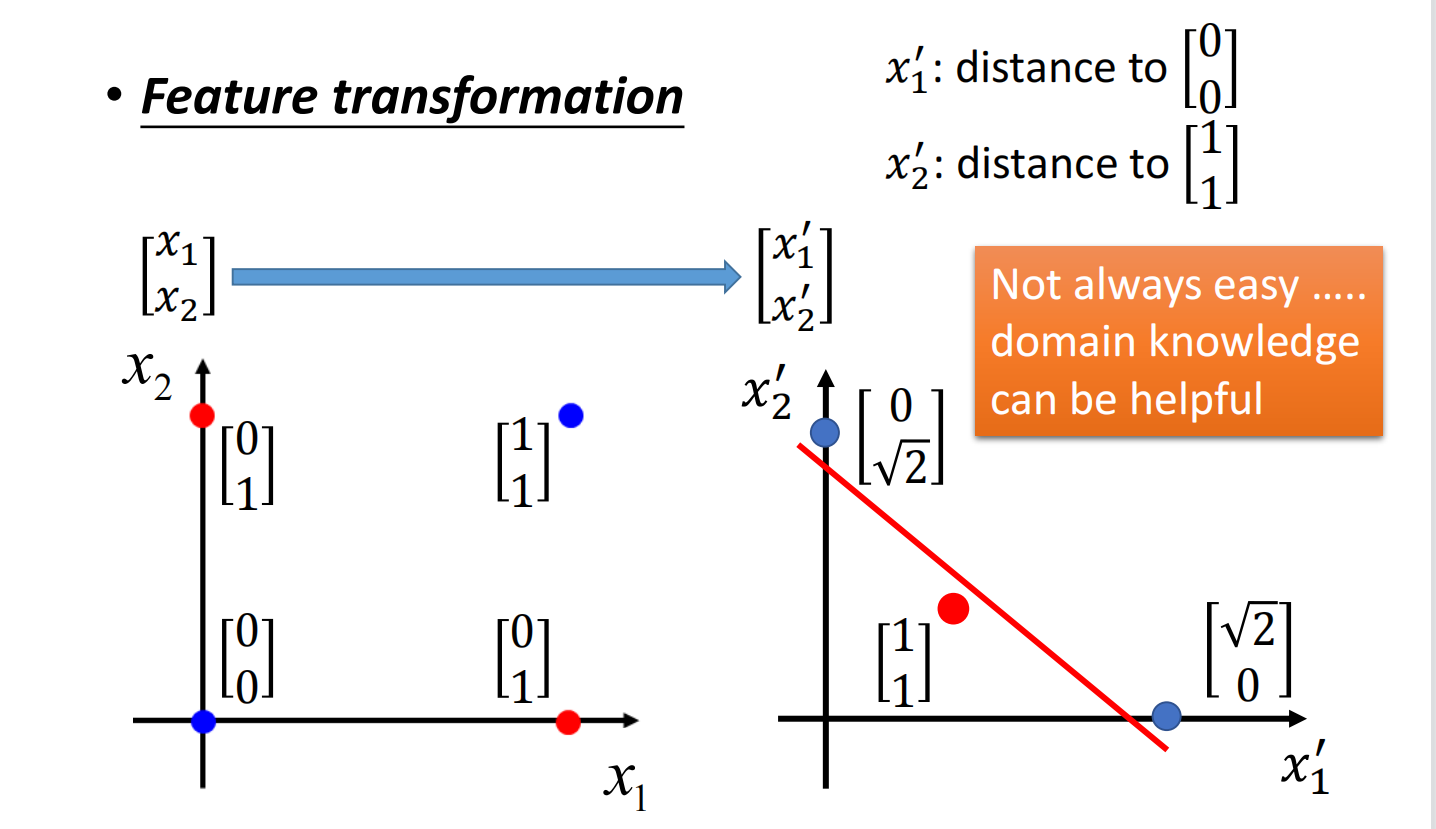
如何让机器自己进行特征变换