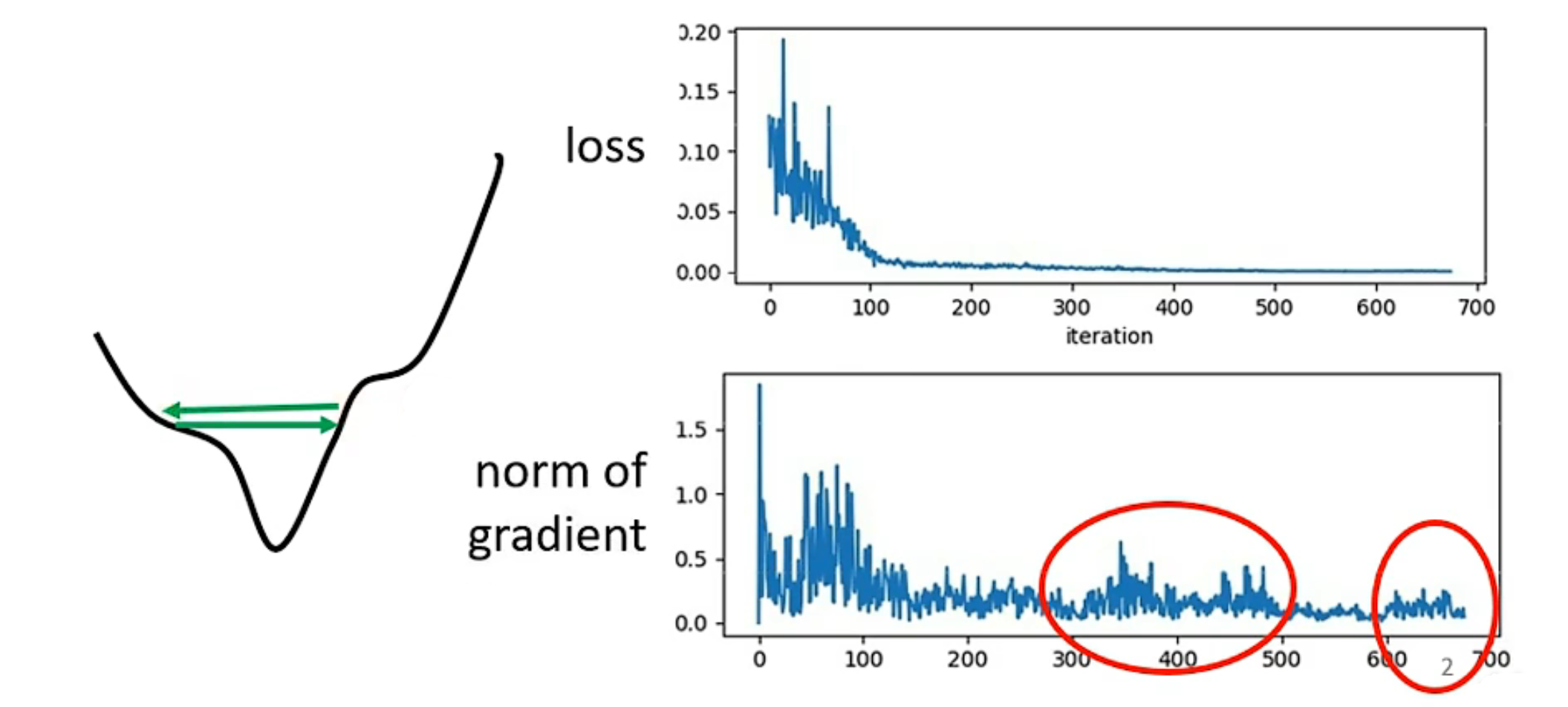
判别模型与生成模型
- 逻辑回归我们可以称他为判别模型(Discriminative)
- 使用高斯分布来描述后验概率我们可以成为生成模型(Generative)
实际上他们的model和function set是一样的,都是 $\sigma(w \cdot x+b)$,通过计算 $w$ 和 $b$ 得到不同的function。
对于二分类
对于判别模型,我们可以之间找出 $w$ 和 $b$
对于生成模型,我们需要先计算出 $\mu^{1}, \mu^{2}, \Sigma^{-1}$,然后把 $w$ 和 $b$ 计算出来
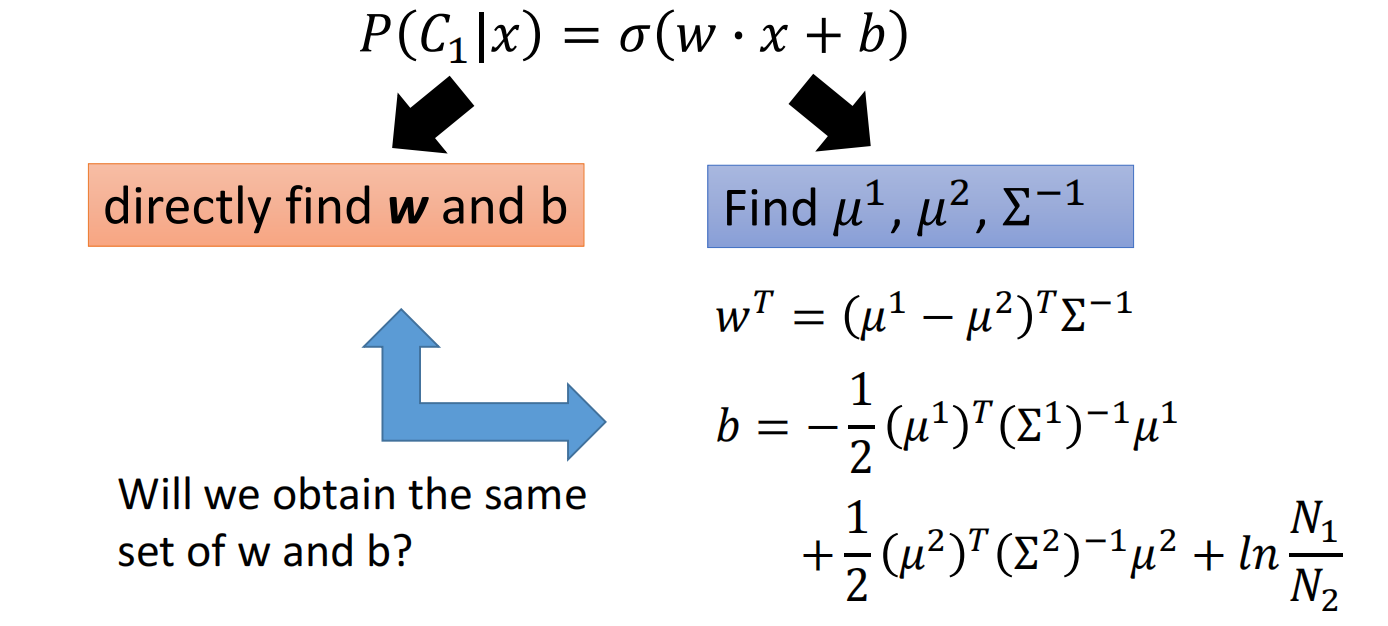
对于两种方法,很有可能会使用同一个模型和function set,得到不同的参数结果
下面比较两种方法的优劣:
对于之前的例子,二者结果如下:
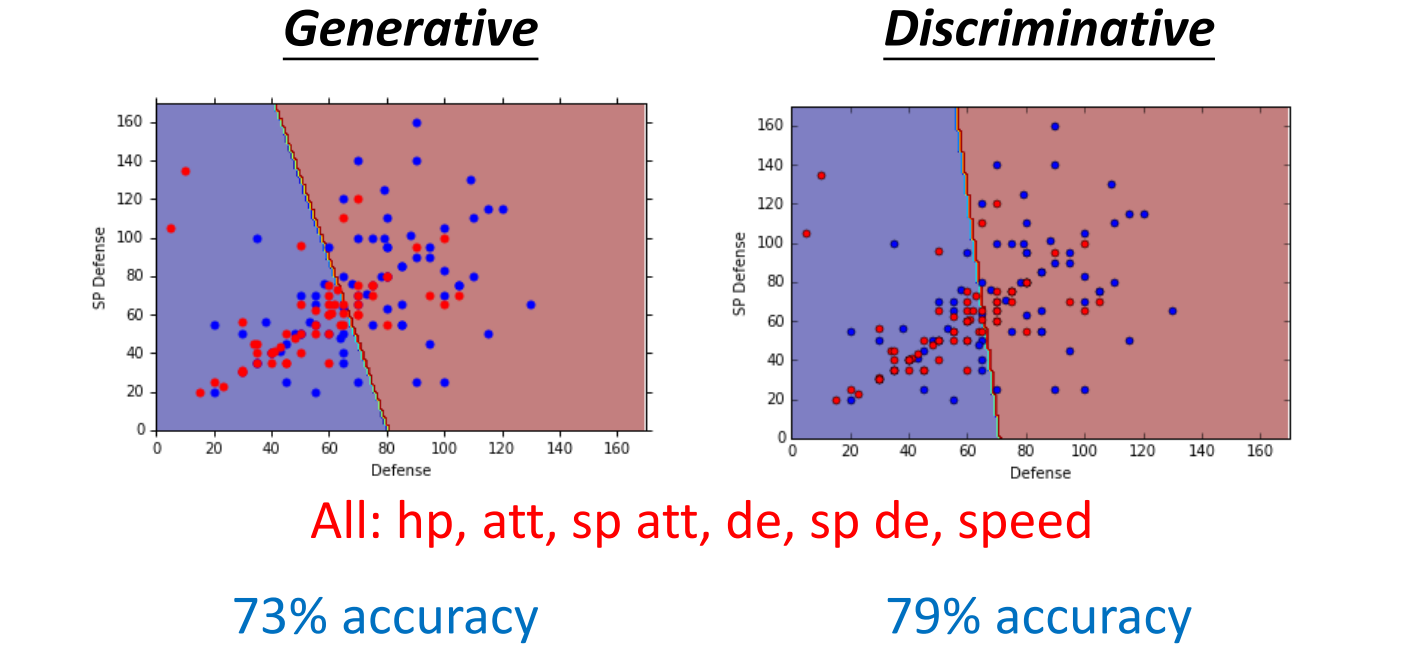
在文献中,常常会有人提到判别模型比生成模型的效果要更好
现在假设我们有两个class,每个data有两个特征,一共有13个data

首先我们使用朴素贝叶斯(native bayes)进行计算:

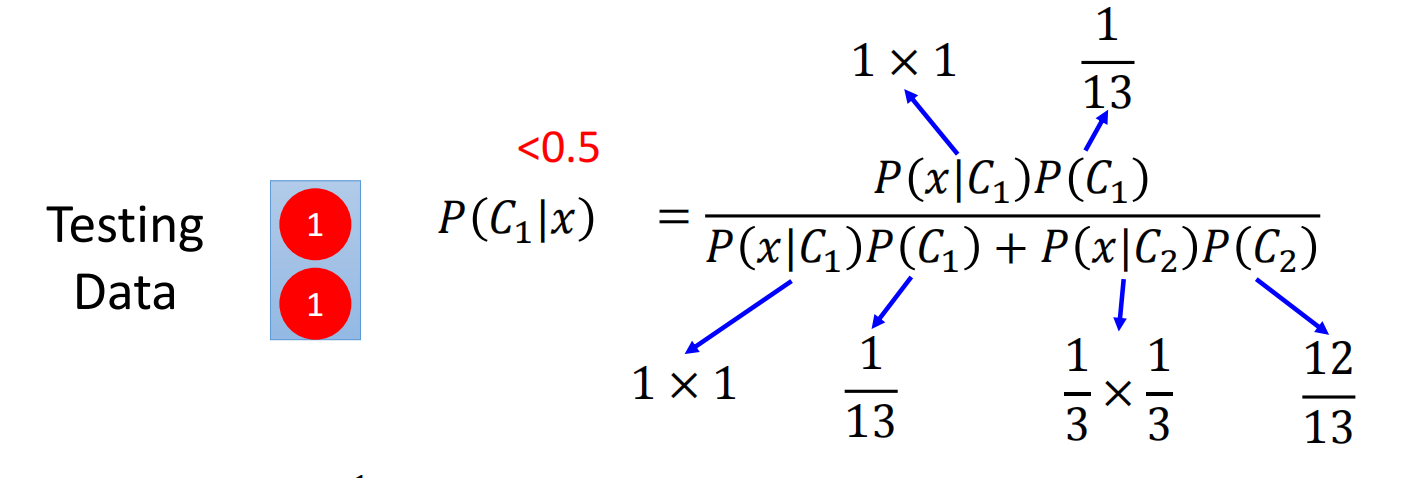
因此,对于朴素贝叶斯来说,测试数据属于class 2而不是class 1,他不考虑不同维度(dimension)之间的相关性(correlation),因此class 1中的两个x是互相独立的
总结
生成模型跟判别模型的不同点在于生成模型做了一定的假设(脑补),如果实际数据不符合先验假设时,生成模型就会出错。
也可以理解为判别模型自动学习特征之间的关系,生成模型假定特征之间符合某种关系
但生成模型有时也会存在优势:
- 采用概率分布的假设
- 对训练数据的需求更小
- 对噪声更加稳健
- Priors and class-dependent probabilities 可以从不同的来源进行估计
例如对于语音识别来说,先验概率不需要有声音的data去训练,语言模型可以通过文字的概率直接统计得出,因此可以把class-dependent和先验分来
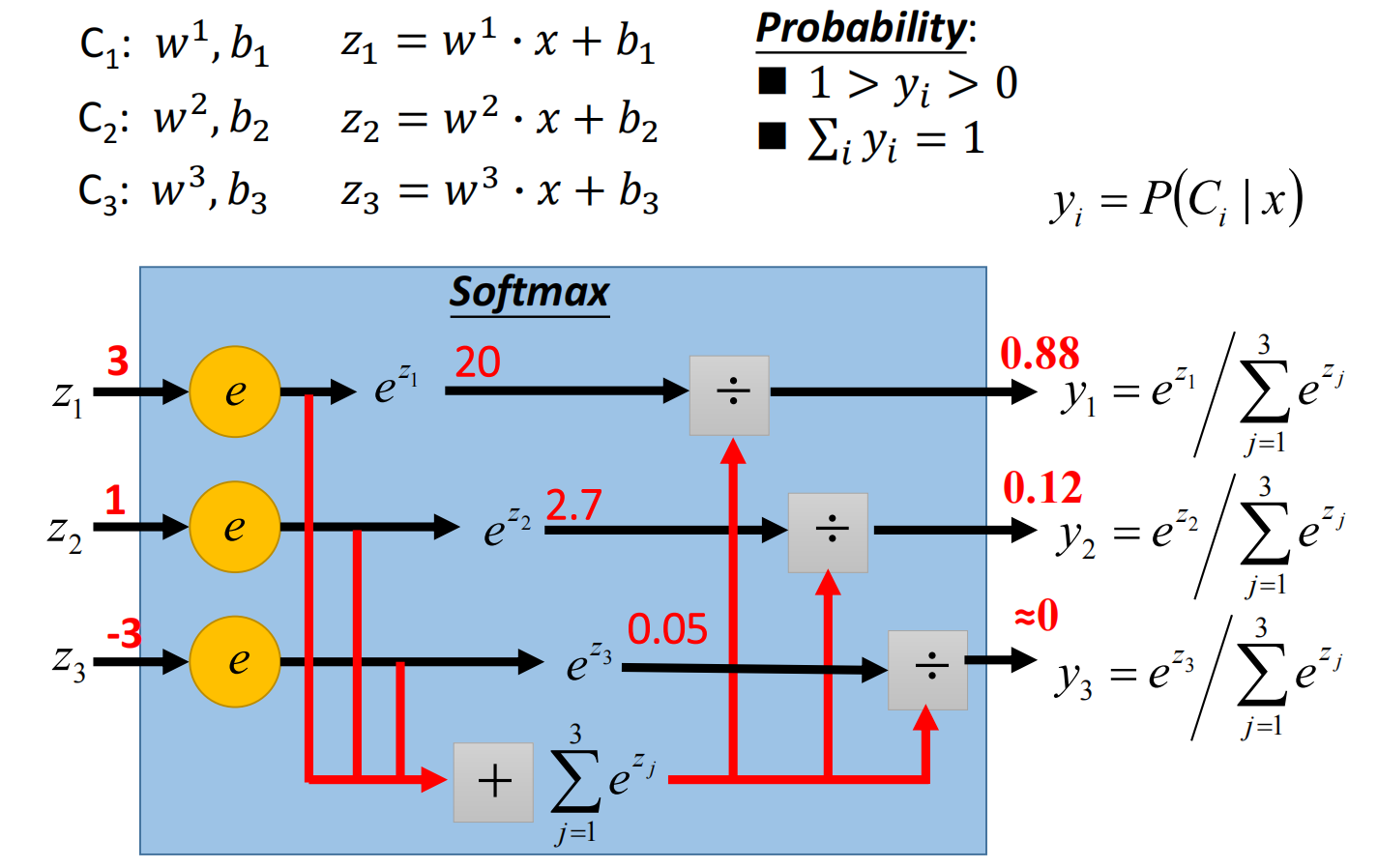
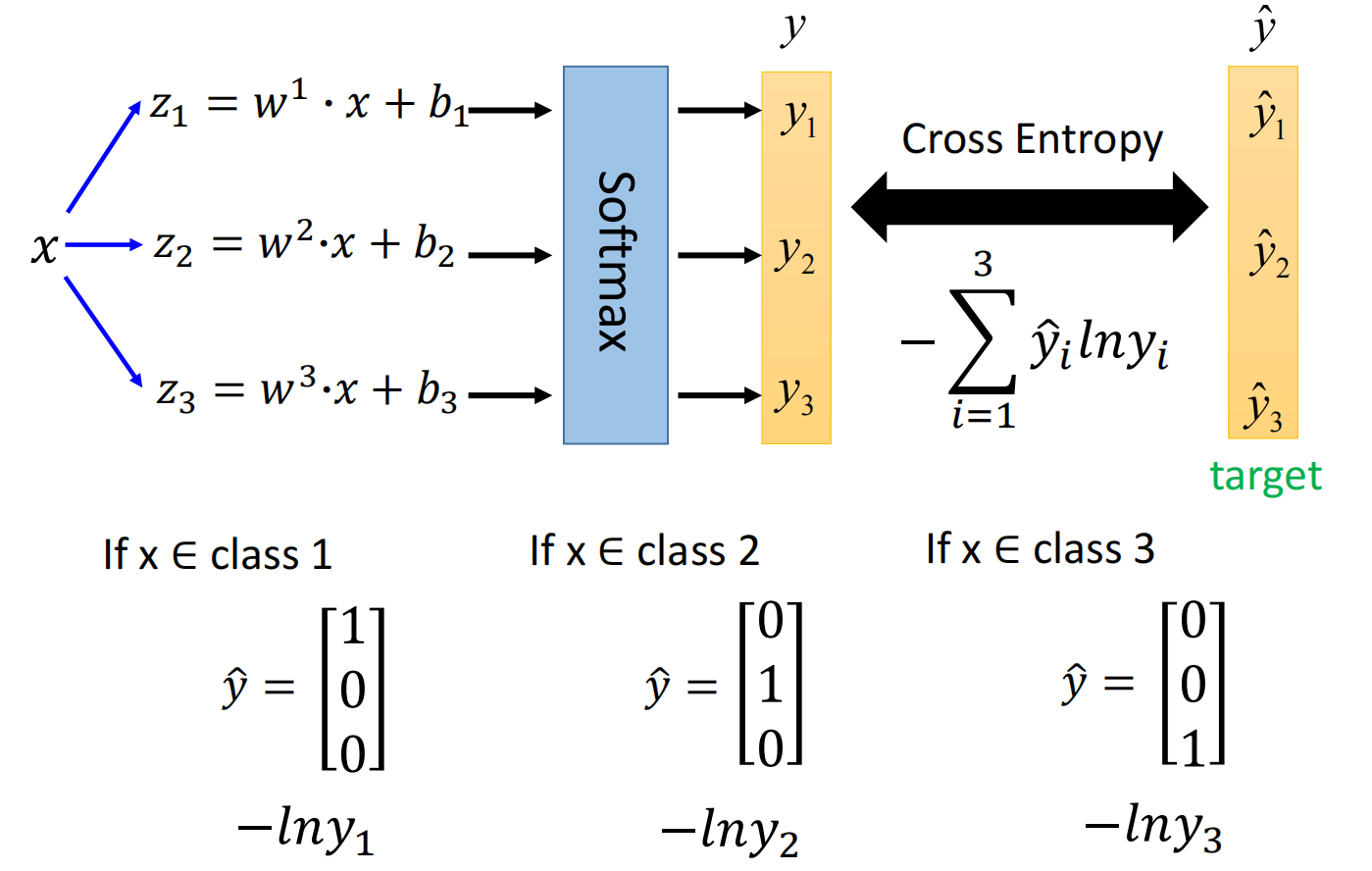
多分类(以3分类为例)
假设有三个class:$C1, C2, C3$, 每组都有自己的weight和bias,对其归一化处理(Softmax)