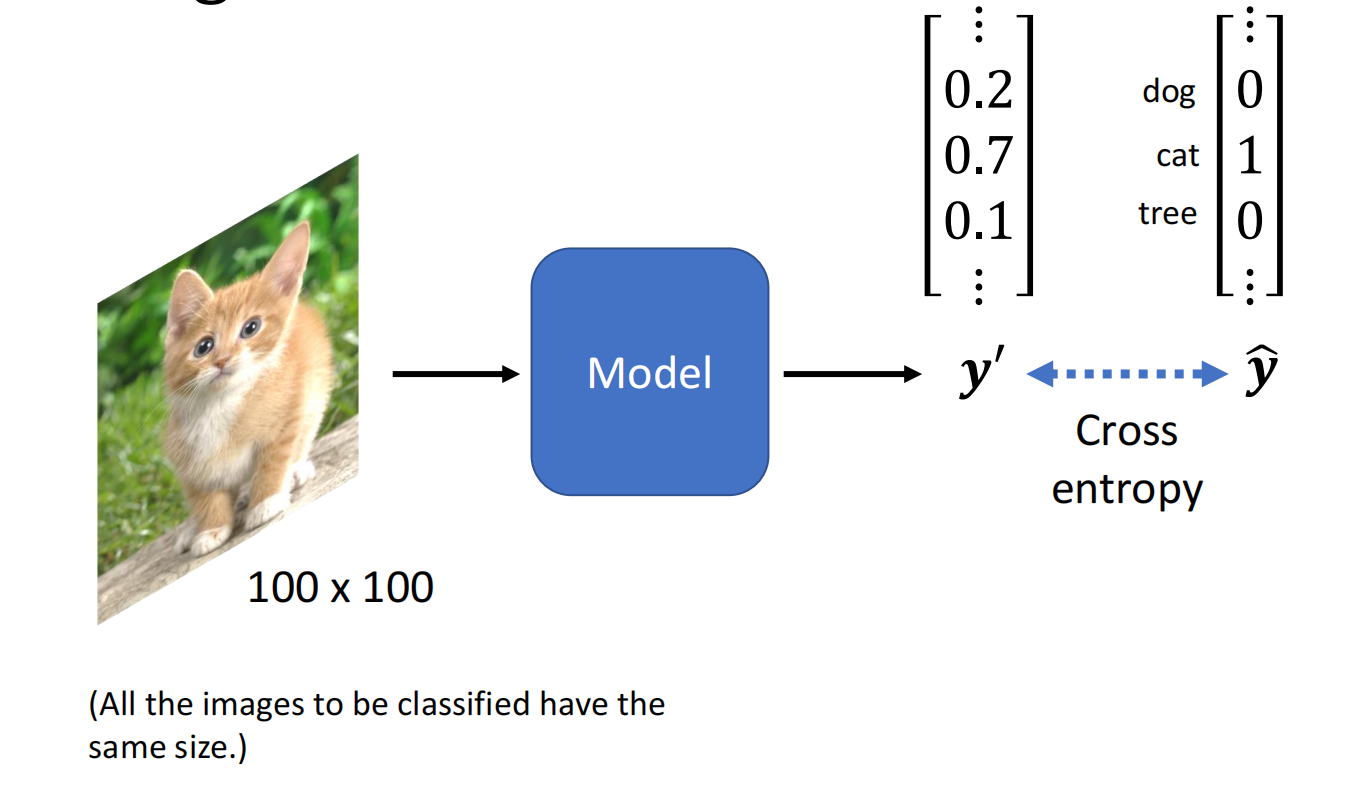
图像识别：输入一张 $100 \times 100$ 的图片，输出识别结果

Introduction 1

对于机器来说，一张图片是一个三维的tensor（长、宽、channel），把矩阵拉直成向量

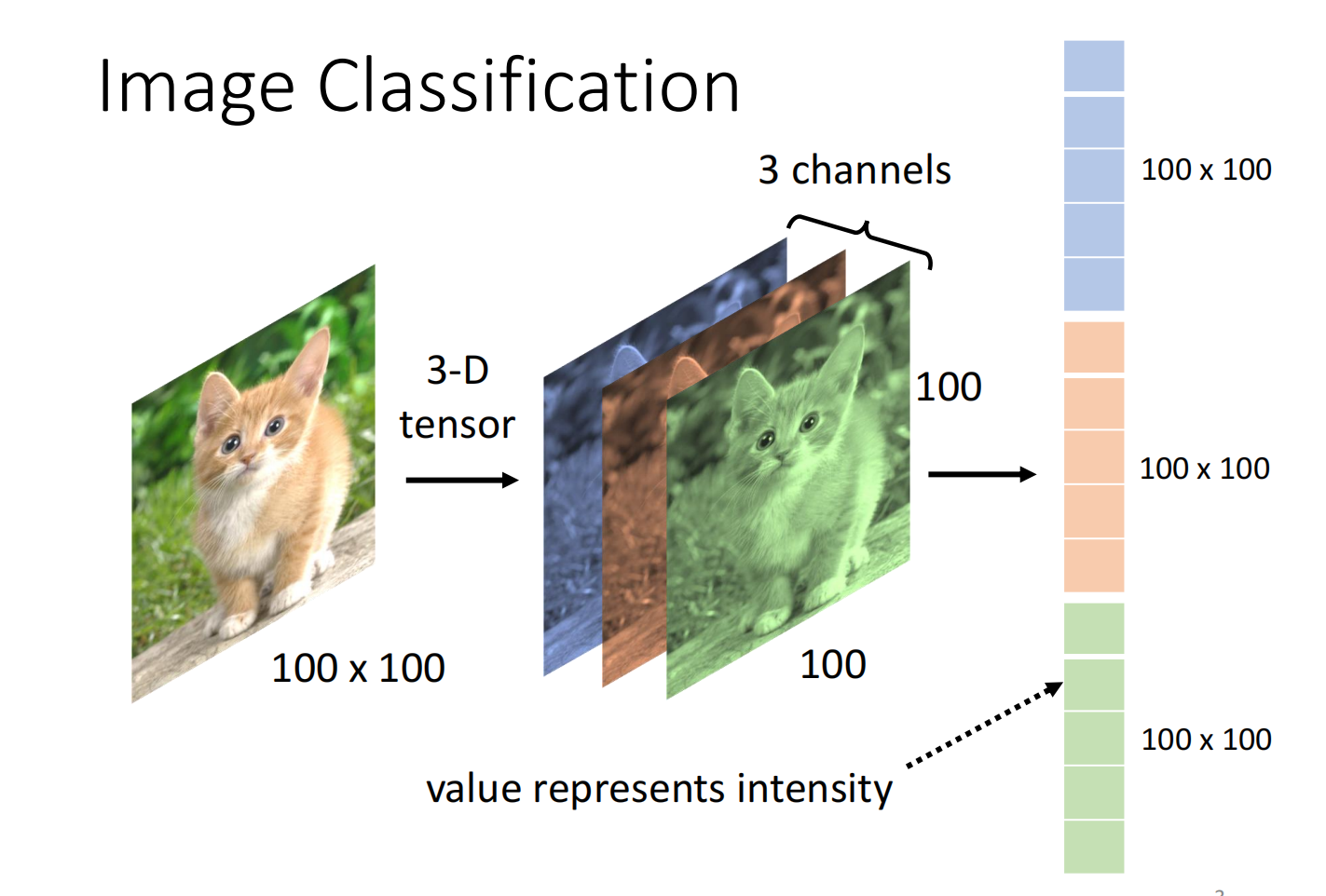
如果我们把它输入到DNN中，会导致参数过多，有过拟合的风险
考虑到图像本身的特性，我们不需要每一个neuron和dimension都有一个weight

Simplification 1: receptive field

第一点：我们可以检测有没有出现一些特别重要的部分，能够代表某种物件

所以不需要把整张图片作为输入，根据这个观察，我们进行第一个简化

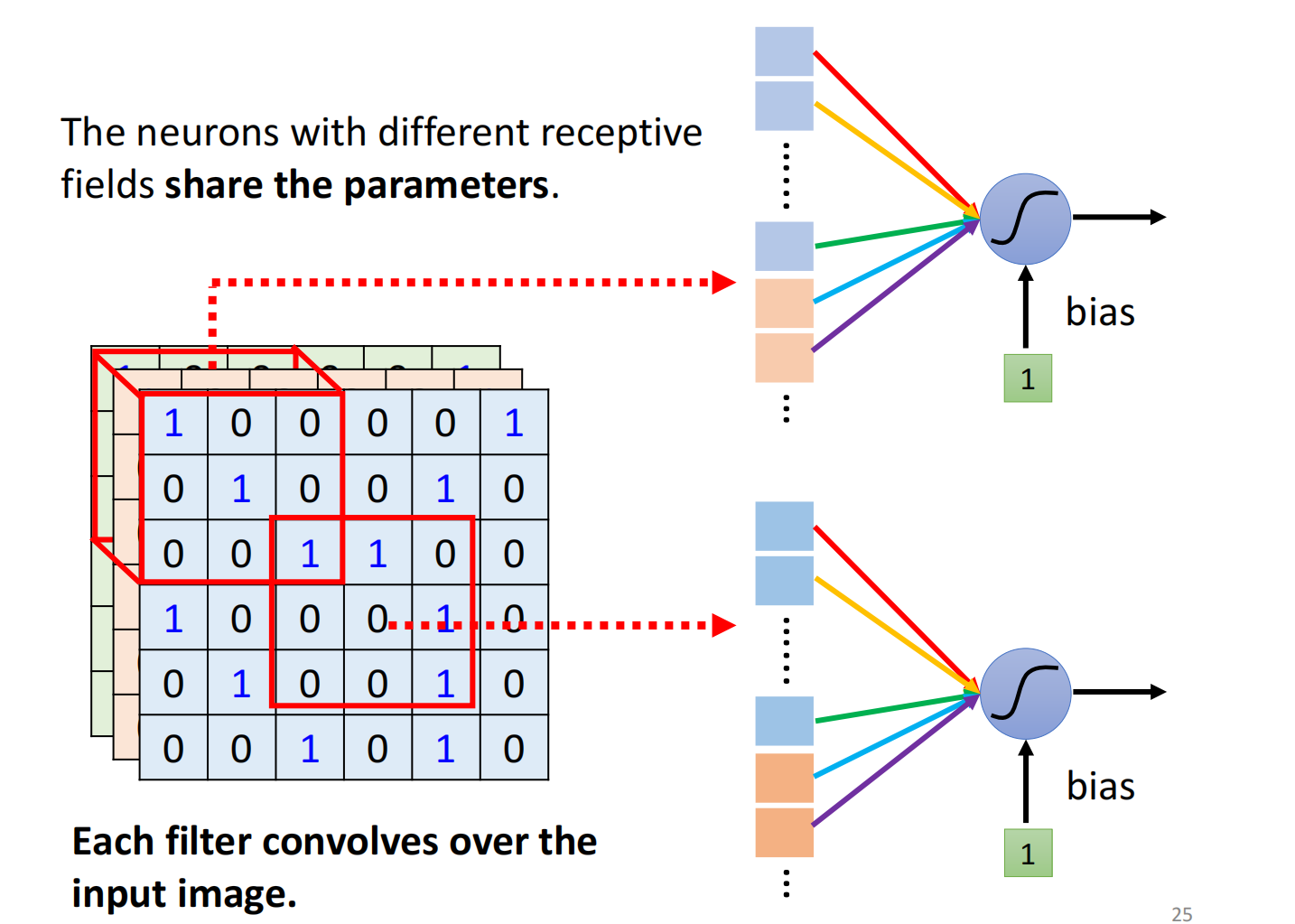
设定一个区域，称之为Receptive Field，每一个Neuron都只关心自己所在的receptive field里面发生的事情，如图所示：

receptive field彼此之间也是可以重叠，同个范围也可以有多个不同的neuron

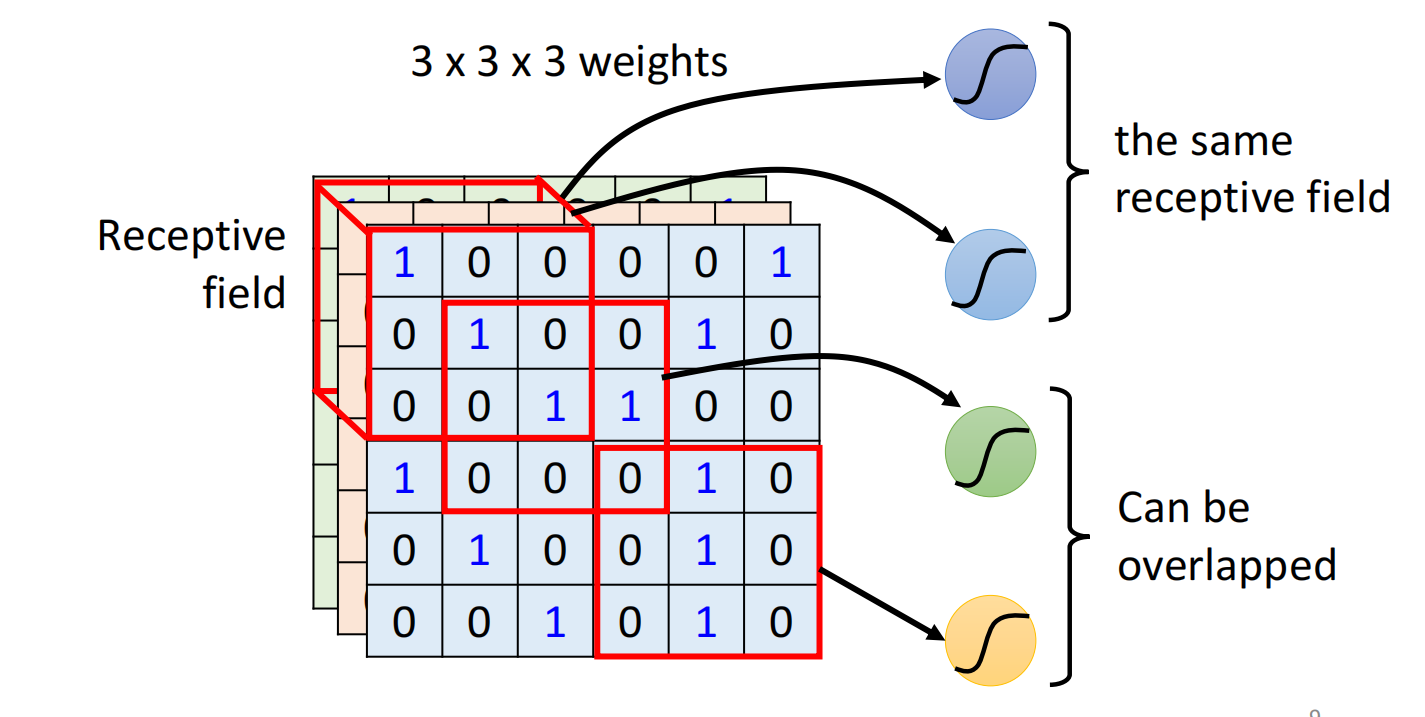
下面是一种最经典的receptive field的安排方式：

• 会看所有的channel，因此我们不用再考虑深度，高跟宽合起来叫做kernel size，kernnel size一般不会设置太大（$3 \times 3$）
• 一般同一个receptive field，会有一组neuron去关注这个范围
• 把一个receptive field移动一定范围形成一个新的receptive field，这个距离称之为stride，也不会设置过大，一般是 $1$ 或者 $2$
• 当receptive field 部分超出了范围时，可以做padding（补0）（补其他值均可）

Simplification 2: parameter sharing

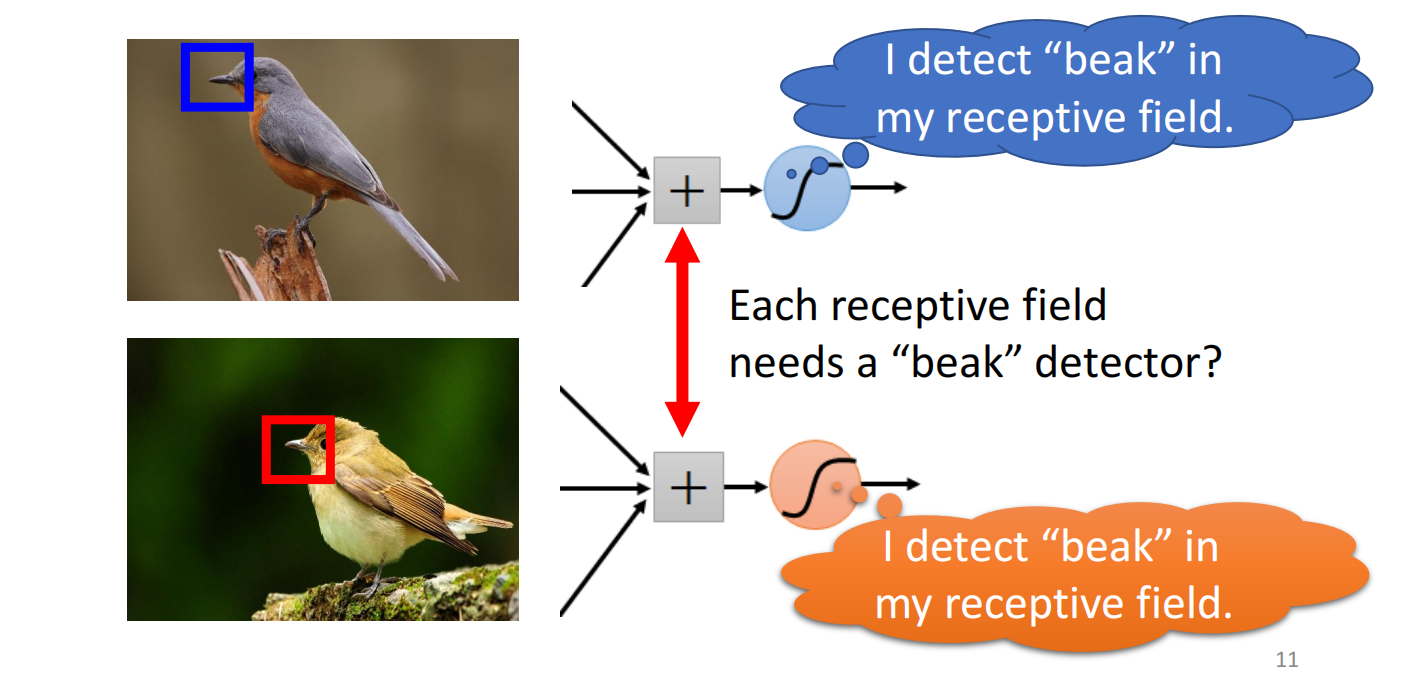
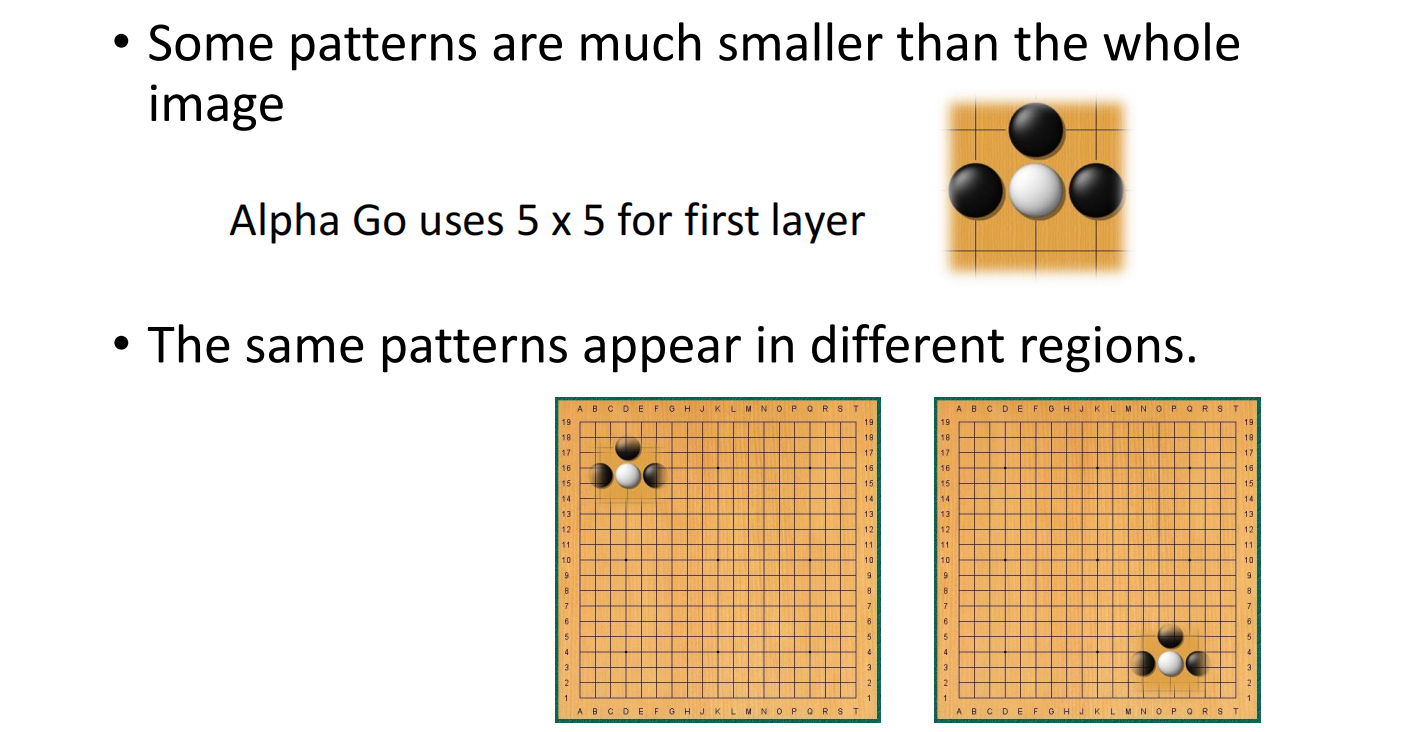
同样的patten可能会出现在图片的不同区域里面

如图所示，这些侦测鸟嘴的Neuron，它们做的事情其实是一样的，只不过他们关注的范围不一样
因此，我们需要每个范围都需要去检测鸟嘴吗？

因此我们想实现：共享参数（parameter sharing）

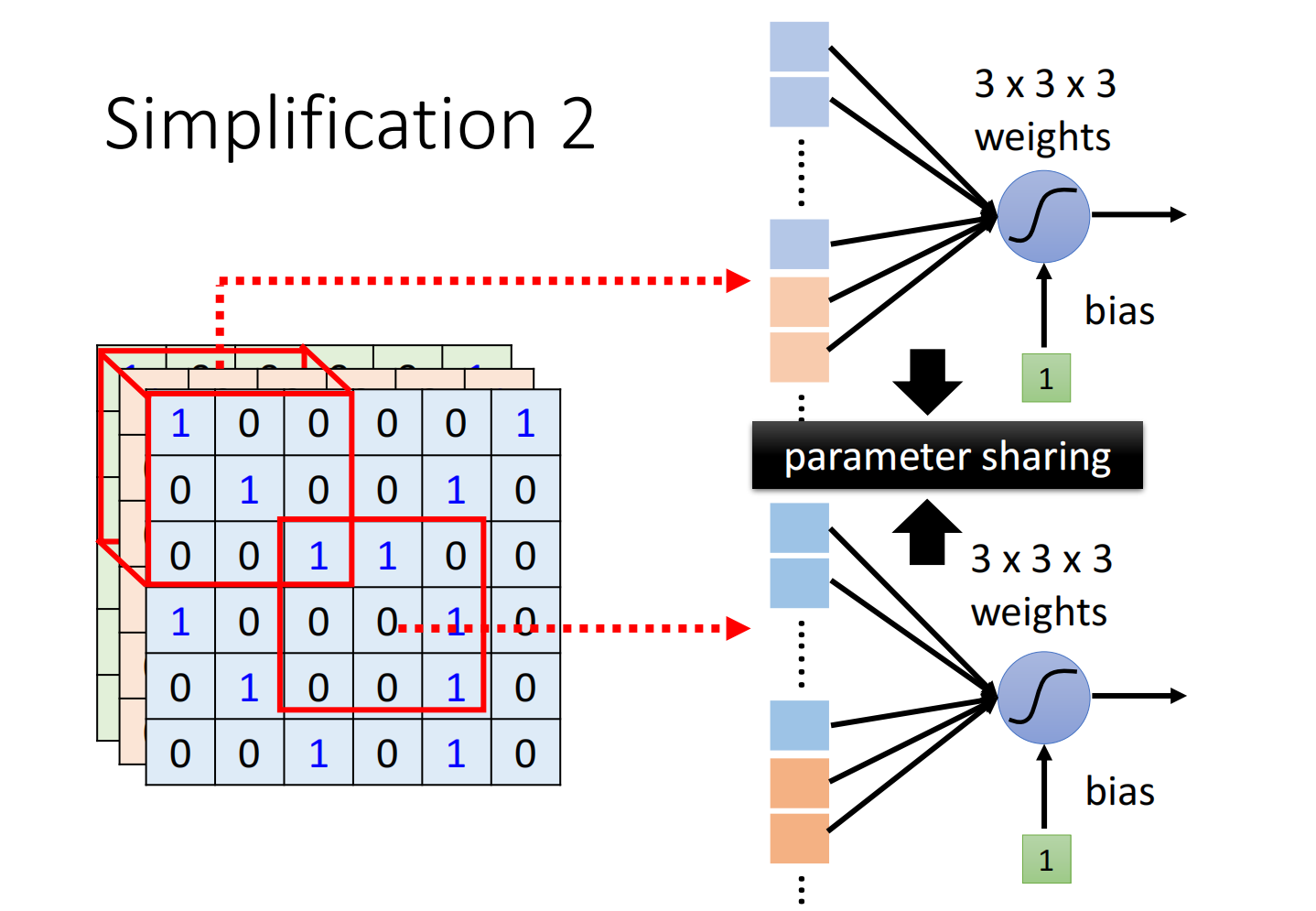
这两个neuron的weight是完全一样的，仅输入不一致（因为位置不同）

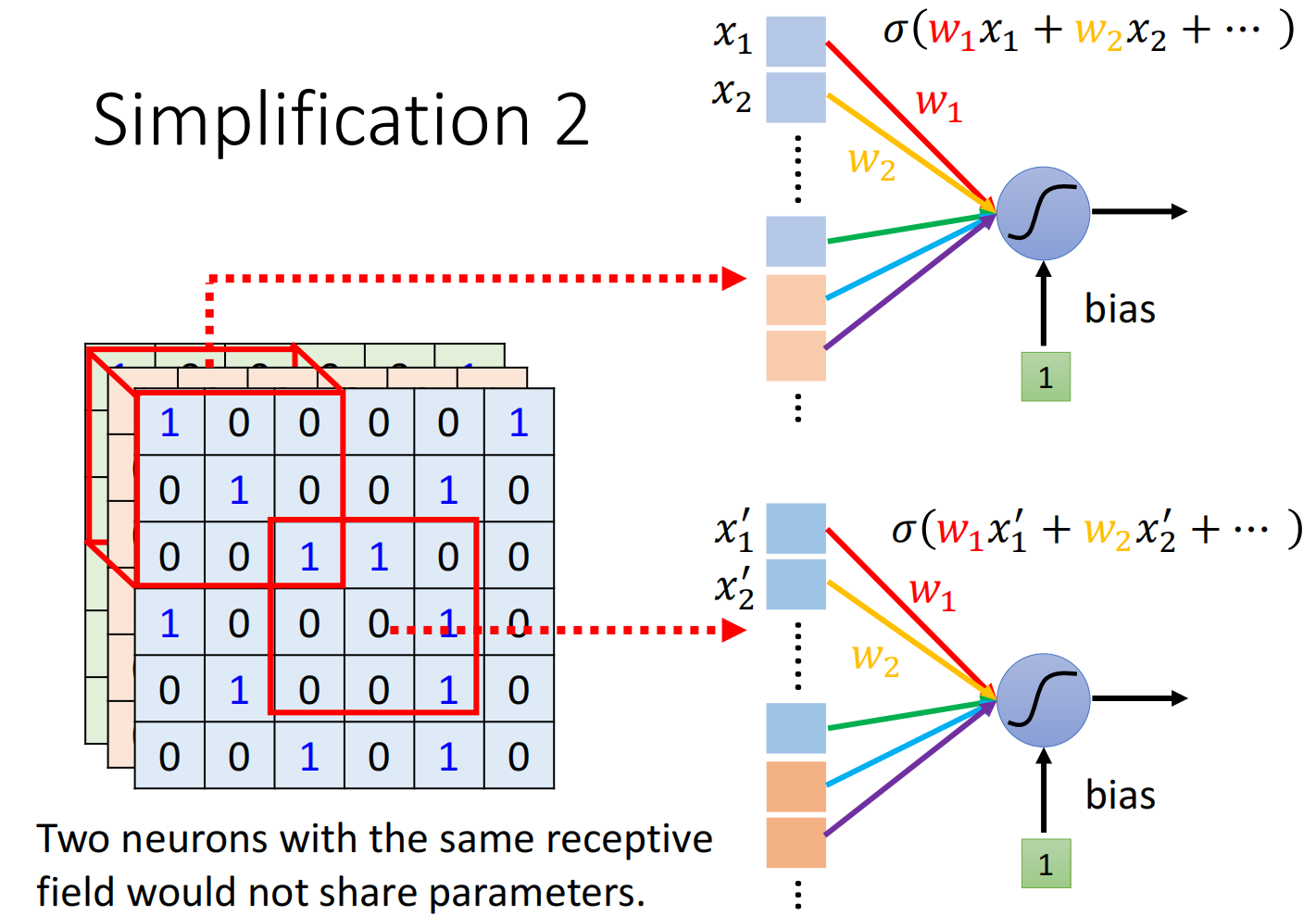
常见的共享参数方法为：

• 每个receptive field都有一组neurons（例如64个）
• 每一个receptive field都只有一组参数，叫做filter，都共用同一组参数

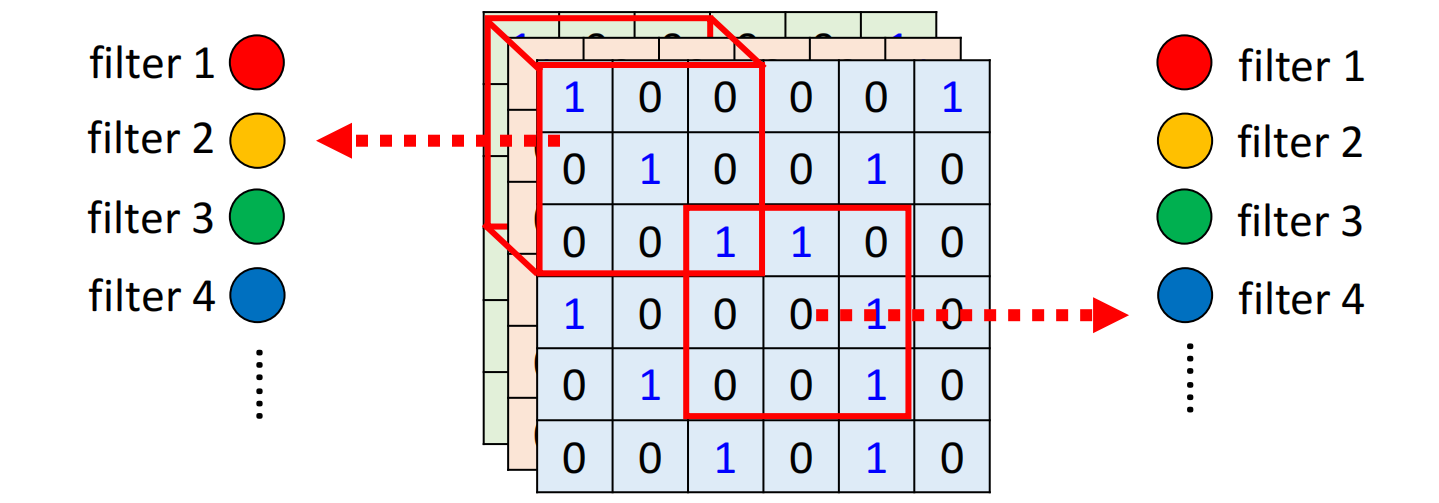
CNN的bias其实是比较大的（不容易overfitting）

Introduction 2

Convolution就是里面有很多的filter，这些filter的大小是 $3 \times 3 \times channel$ ，每一个filter的就是要去抓取pattern

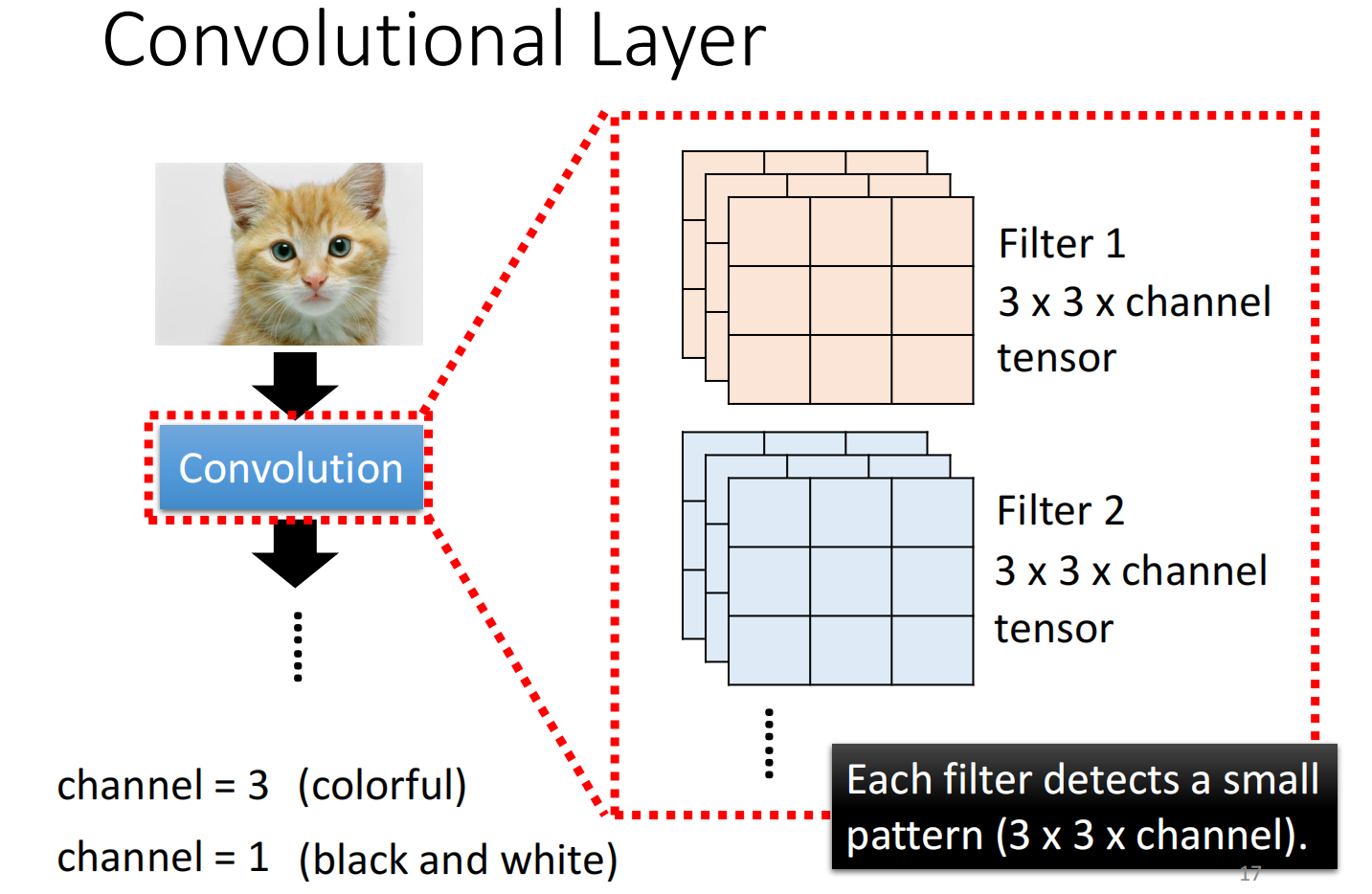
先假设channel 为1，filter的参数已知，其实这些参数的值就是model里面的parameter（实际上filter的数值需要通过gradient decent去寻找）

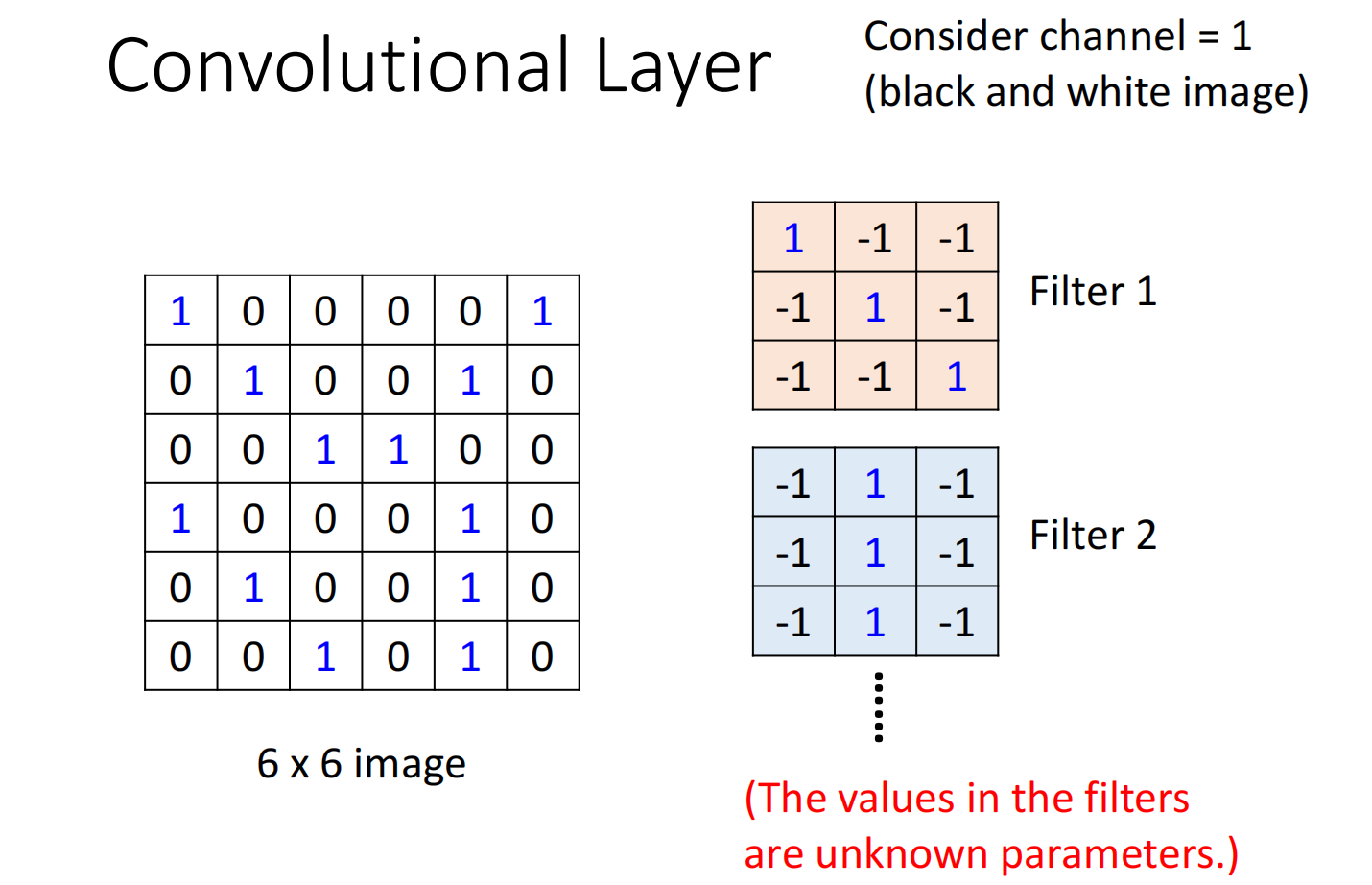
把这个filter跟图片中的9个值做inner product

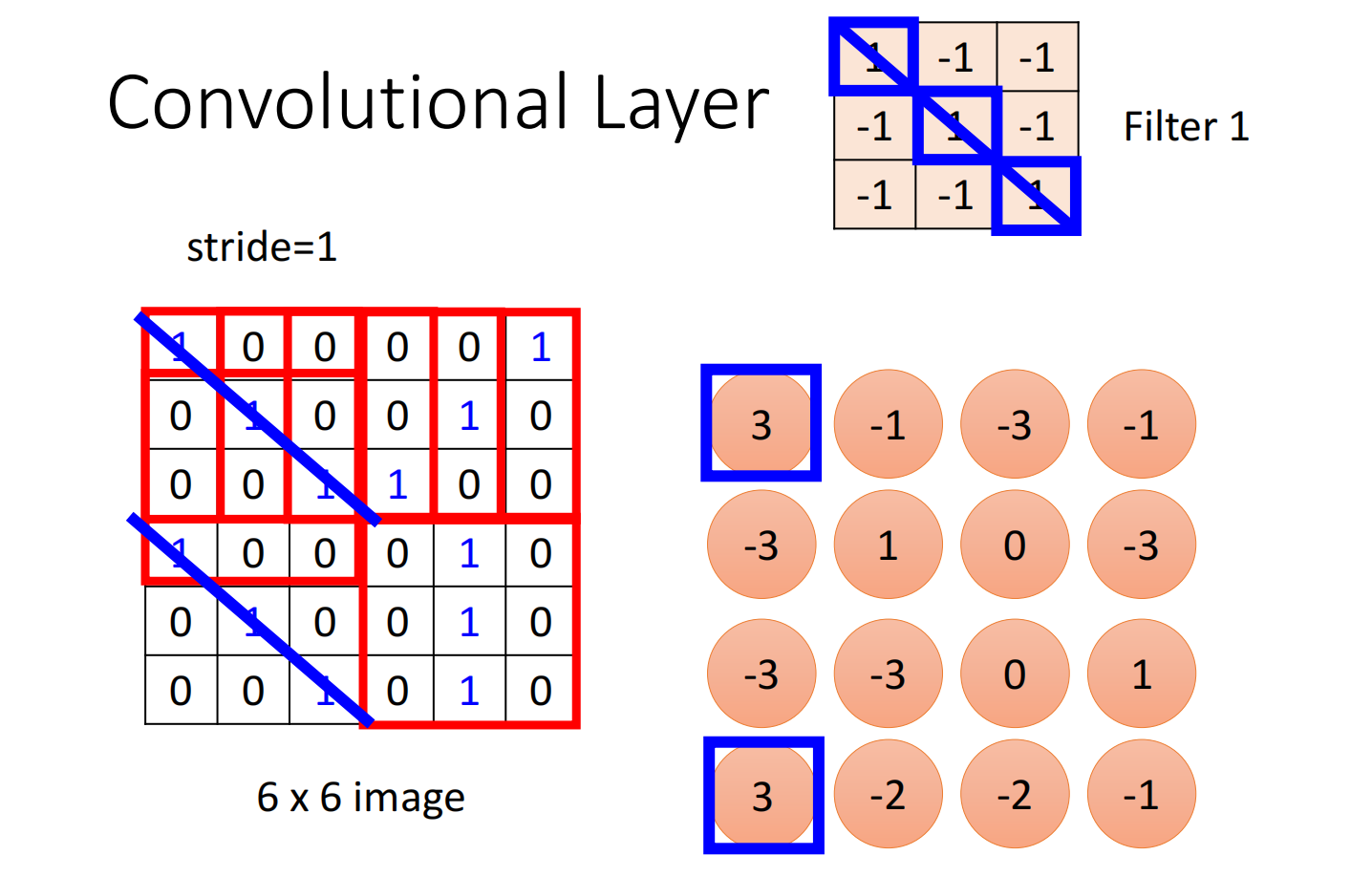
把每个filter都以此类推

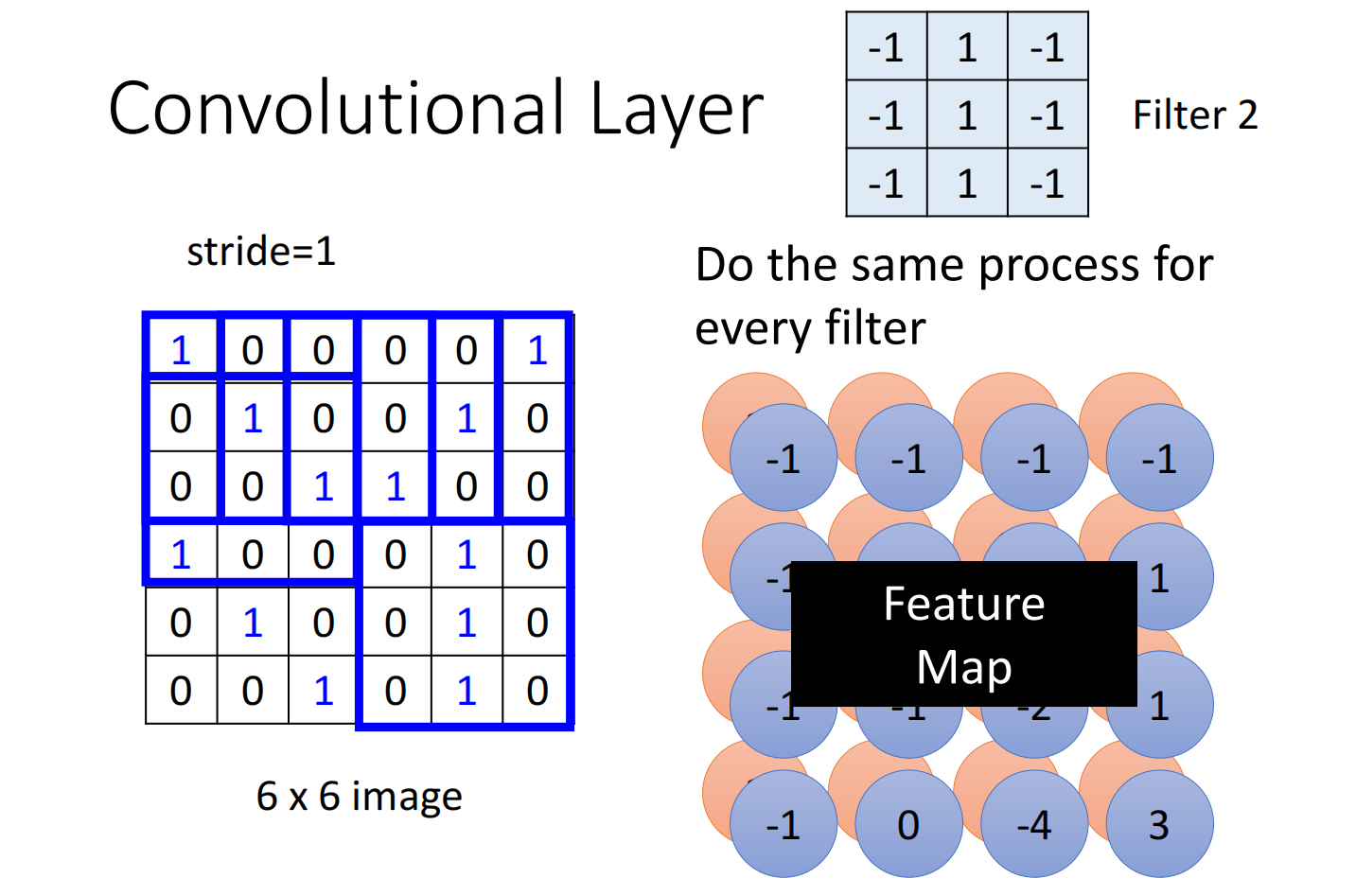
这些结果称之为feature map，我们可以把它看作为一个新的图片，只不过这个图片的channel不是RGB图片的channel，而是每一个channel就是一个filter

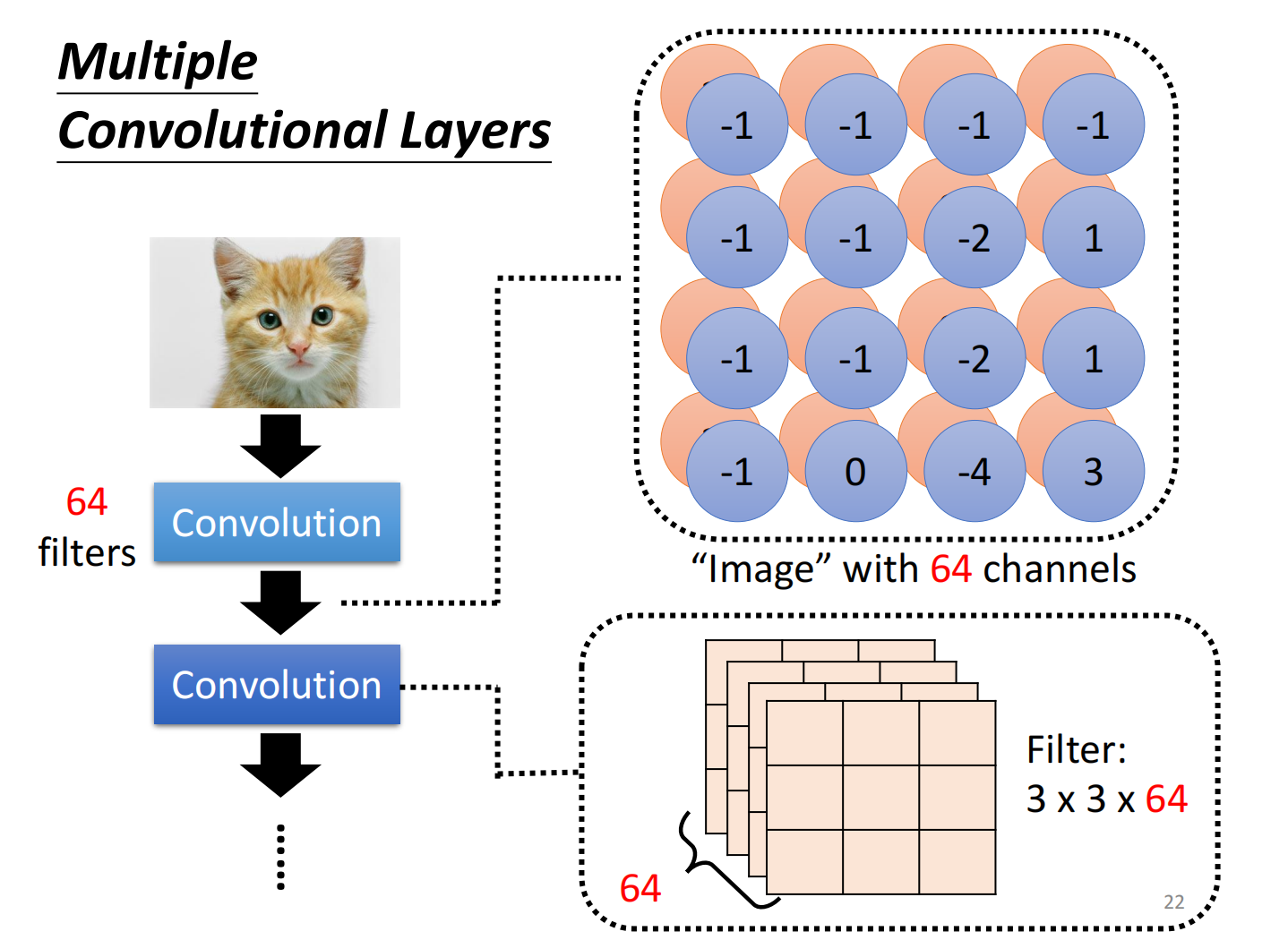
因此network叠的越深，filter能看到的patten越大

第一个里的共用参数其实就是这里的filter

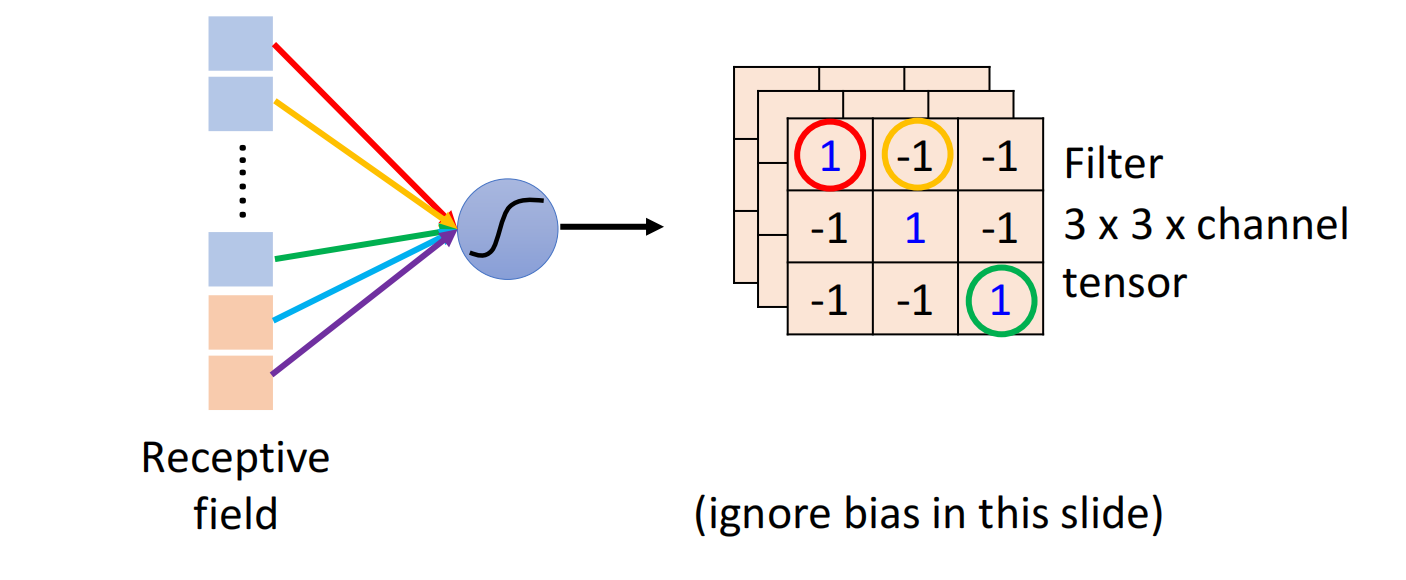
不同的neuron可以share wait，关注不同的范围，这个其实就是把filter扫过一张图片，这个就称之为convolution

Pooling

我们把一张较大的图片做subsampling，比如我们去除奇数列，偶数行，图片大小为原来 $1/4$ ，但实际不会影响图片内容

因此可以降低计算量

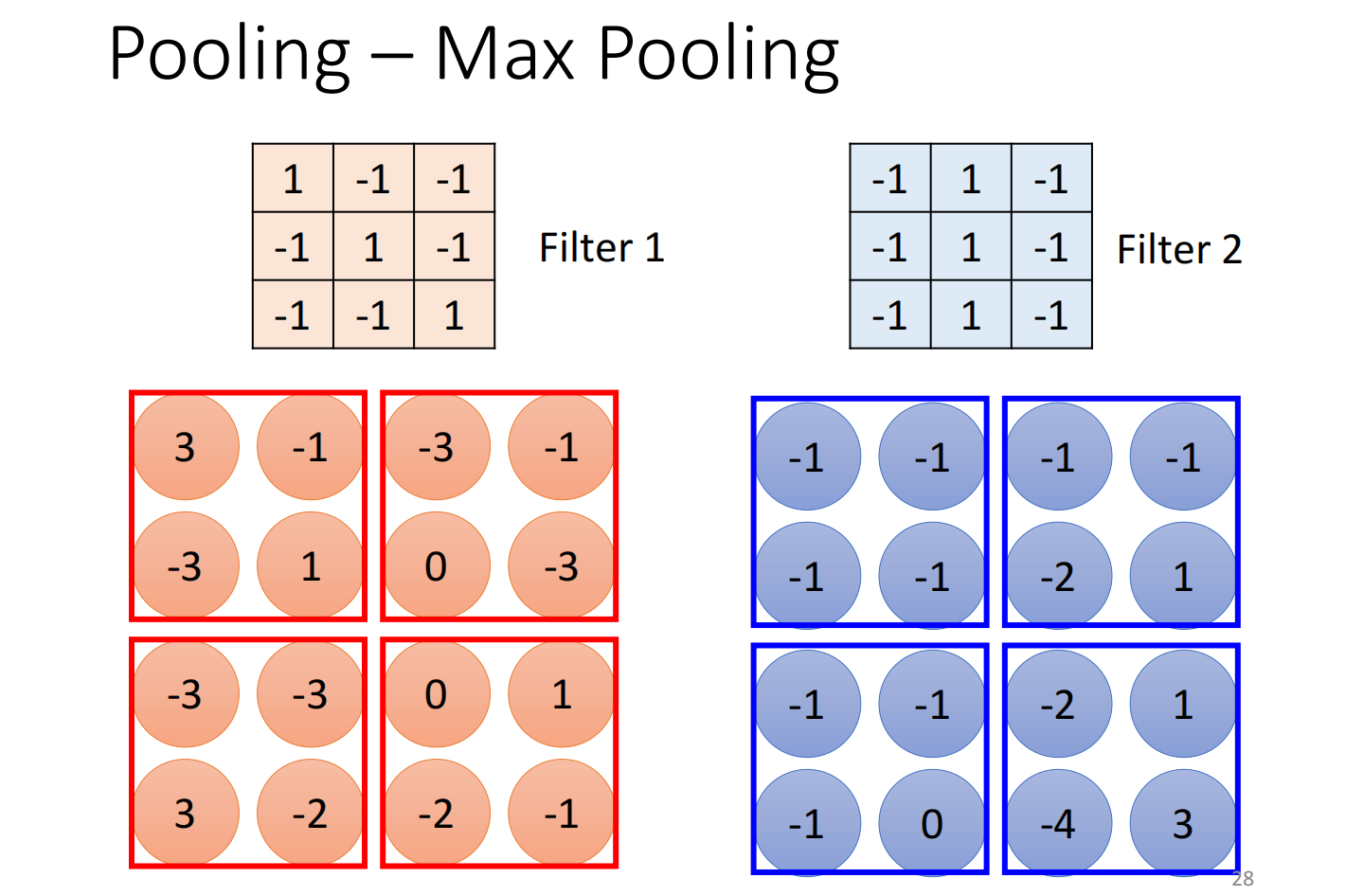
Max Pooling将数字几个一组，选一个代表，在max pooling 中选择最大的那个，即pooling是针对已经被filter处理过后的数据进行缩小化

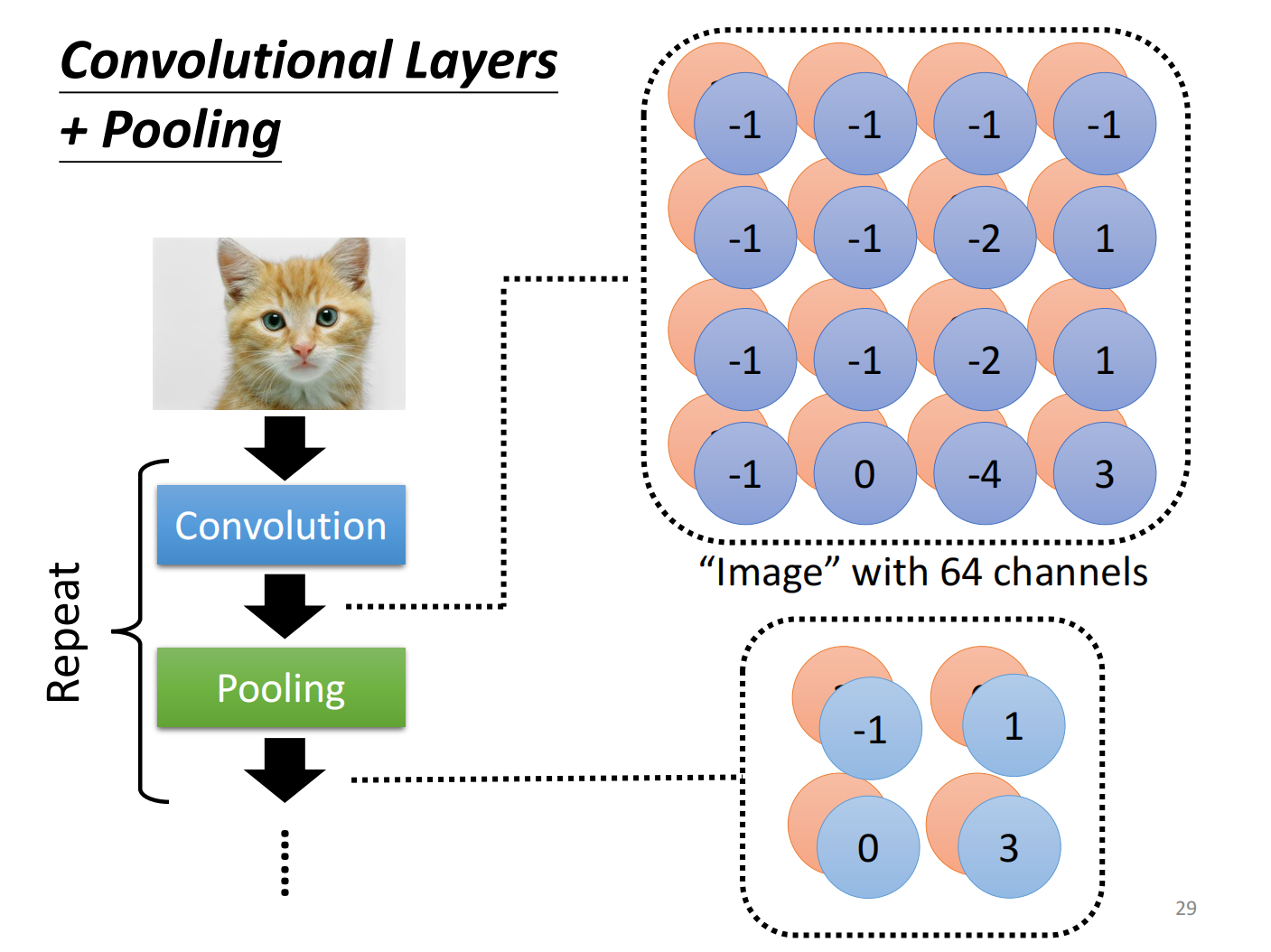
在实际中我们会将convolution 和 pooling 交替使用
但pooling会丢失图片里面的细节，尤其是你需要观察一些很细微的东西
所以近年来很多神经网络的设计开始丢弃pooling，做full convolution的网络

Summary

Flatten就是把矩阵拉直，变成一个向量

最后我们再把向量丢入到Fully Connected Layers进行训练，可能还要再过一个Softmax

除了影视之外，围棋也可以使用CNN

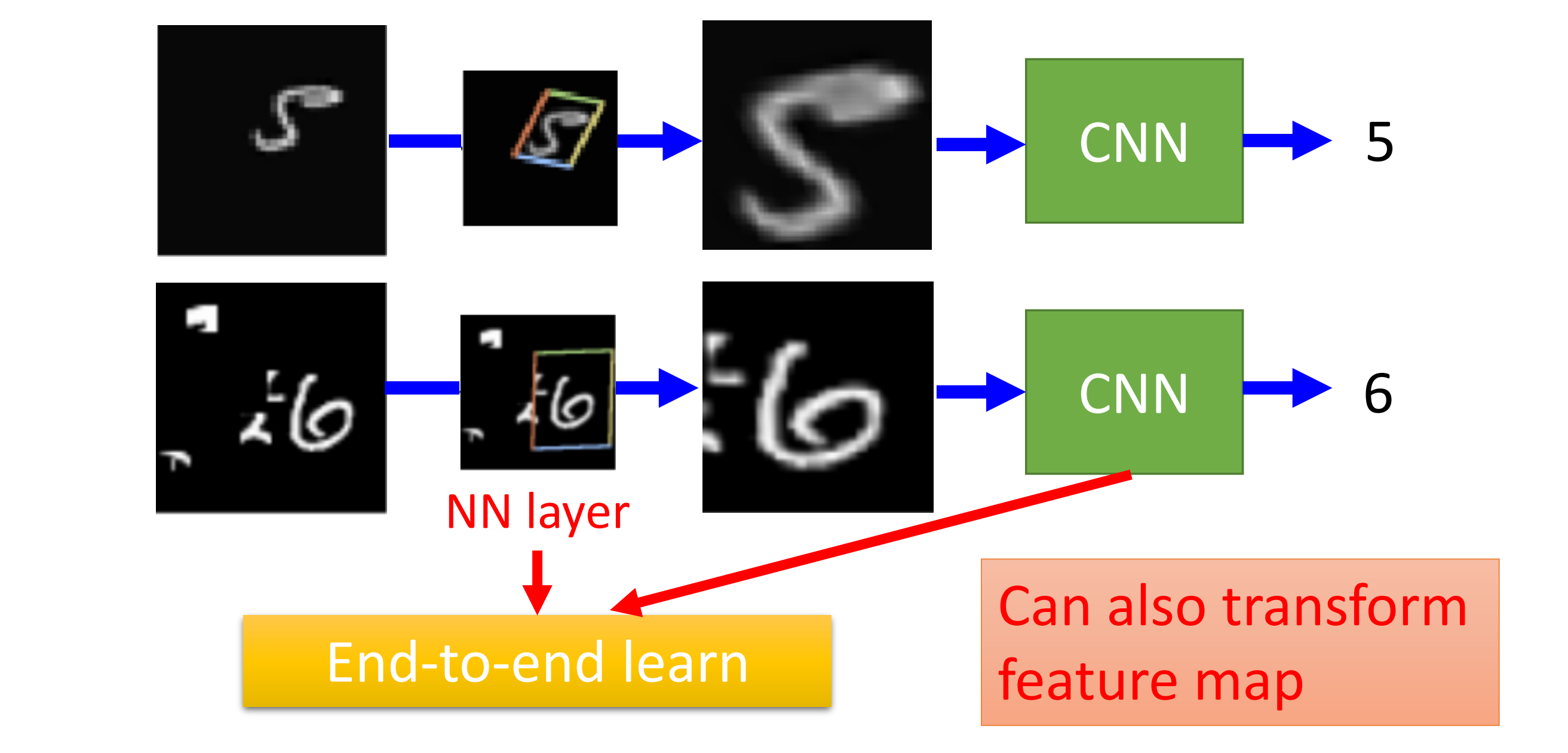
CNN没有办法处理影响影像放大缩小或者旋转的问题
因此我们可以使用Spatial Transformer Layer去解决这个问题