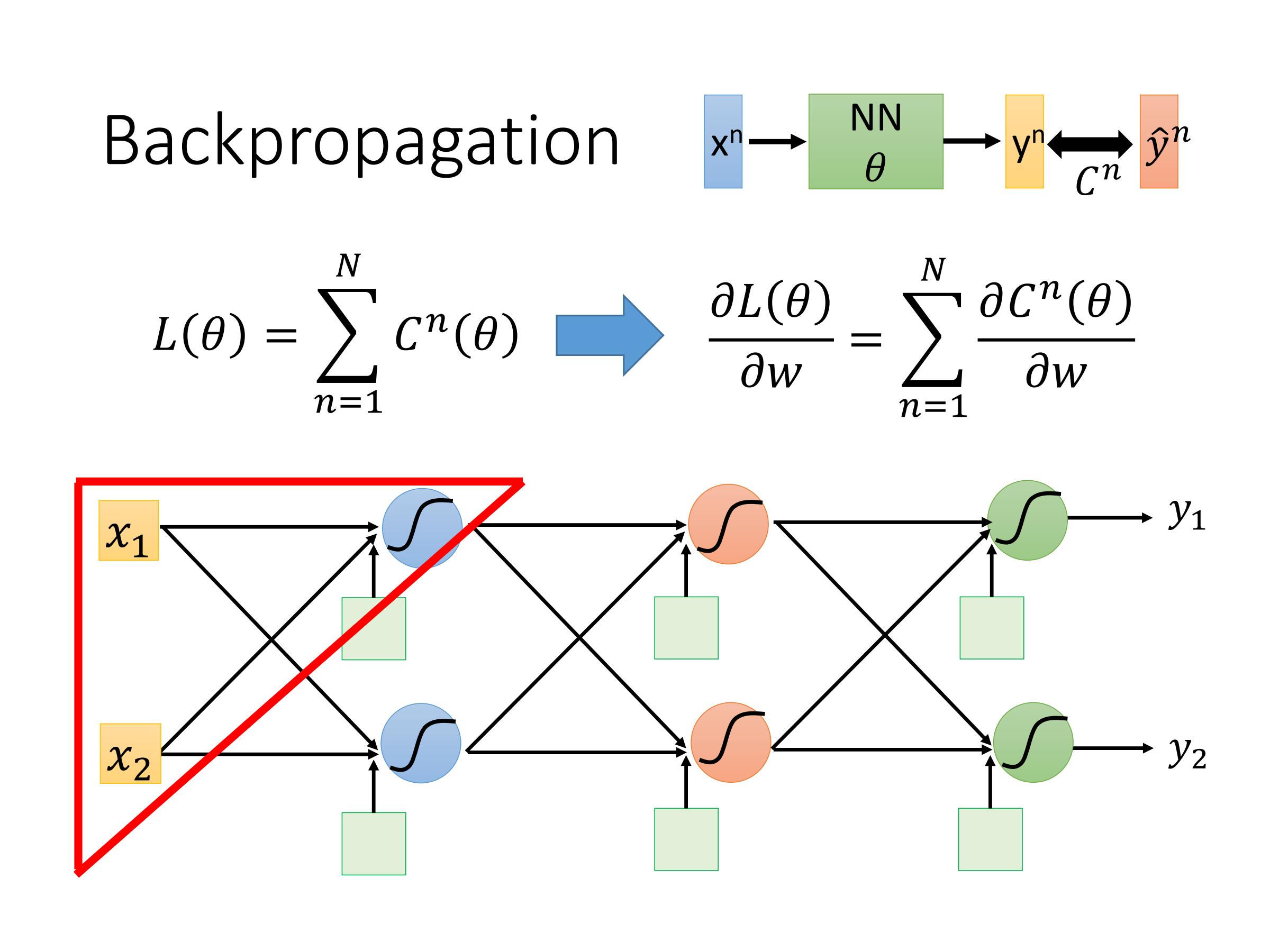
为了更好的计算梯度下降，我们使用反向传播算法

梯度下降 (Gradient Descent)

$L(\theta )$ ：损失函数 (Loss function)

问题在于$\bigtriangledown L(\theta )$可能是一个百万维的向量，现在如何去有效的把它计算出来，因此我们使用反向传播

$C^n$代表$y^n$和$\widehat{y}^n$之间的距离，其实就是预测值和真实值之间的差距，因此$C^n(\theta)$越小越好

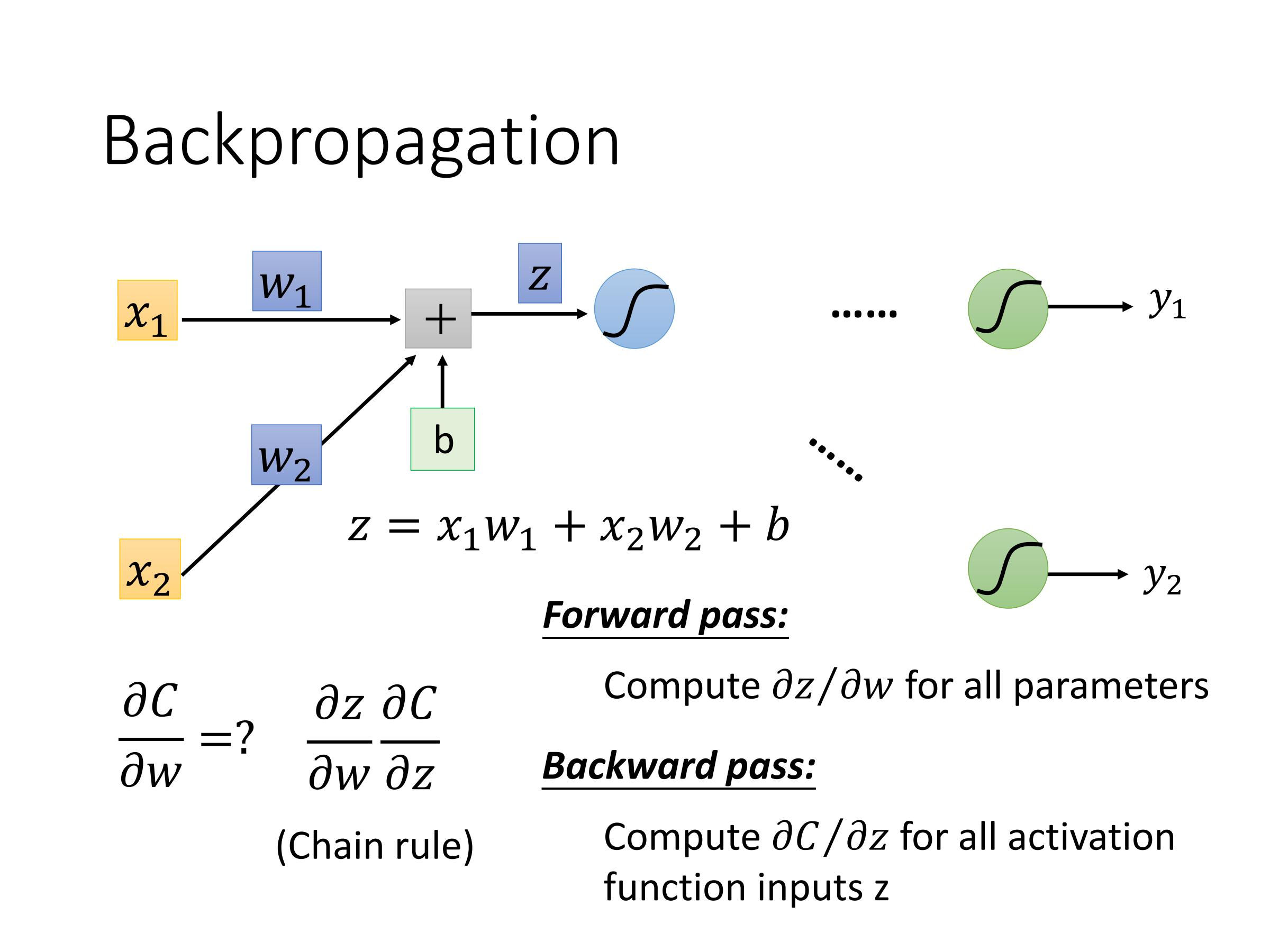
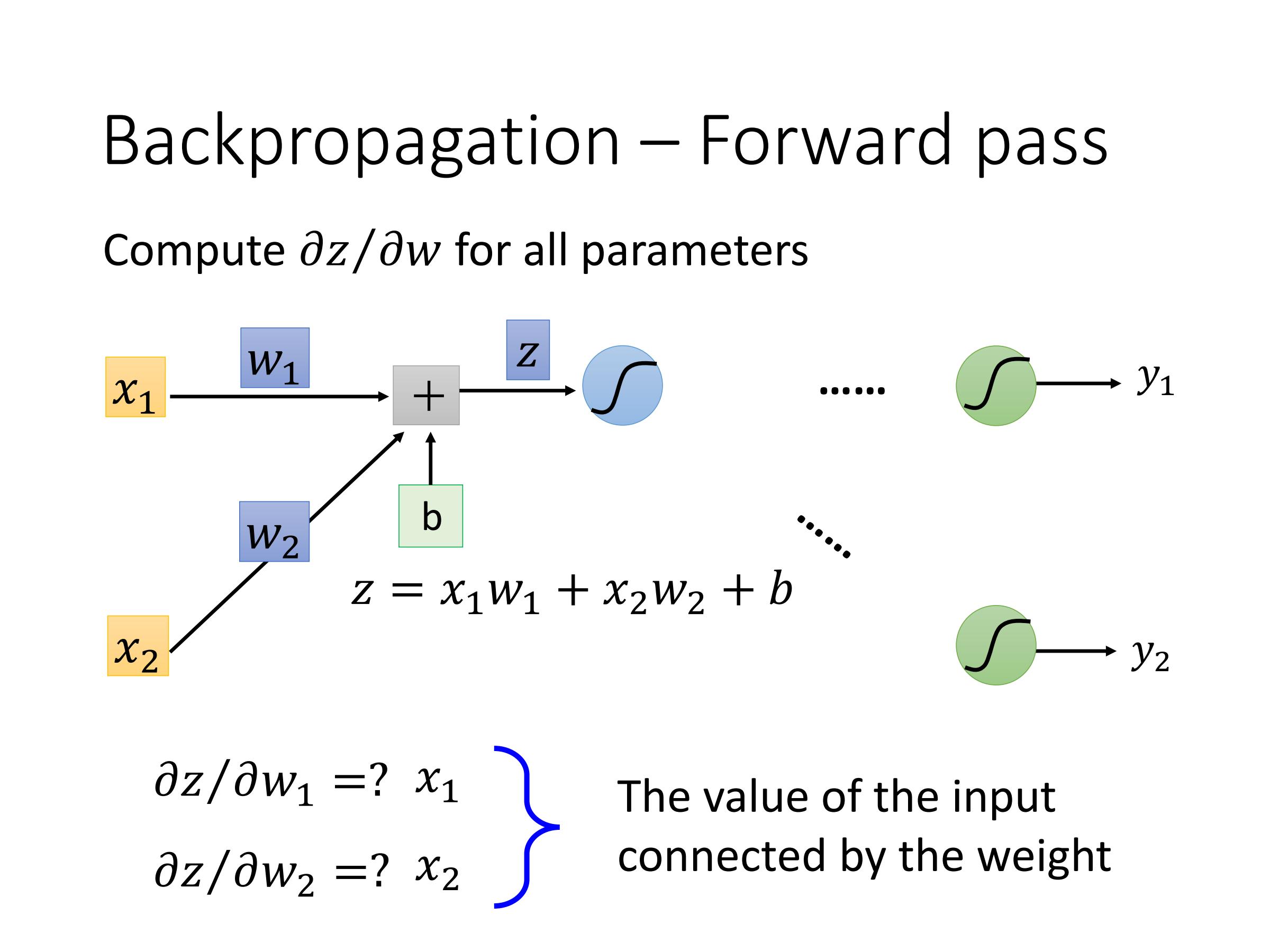
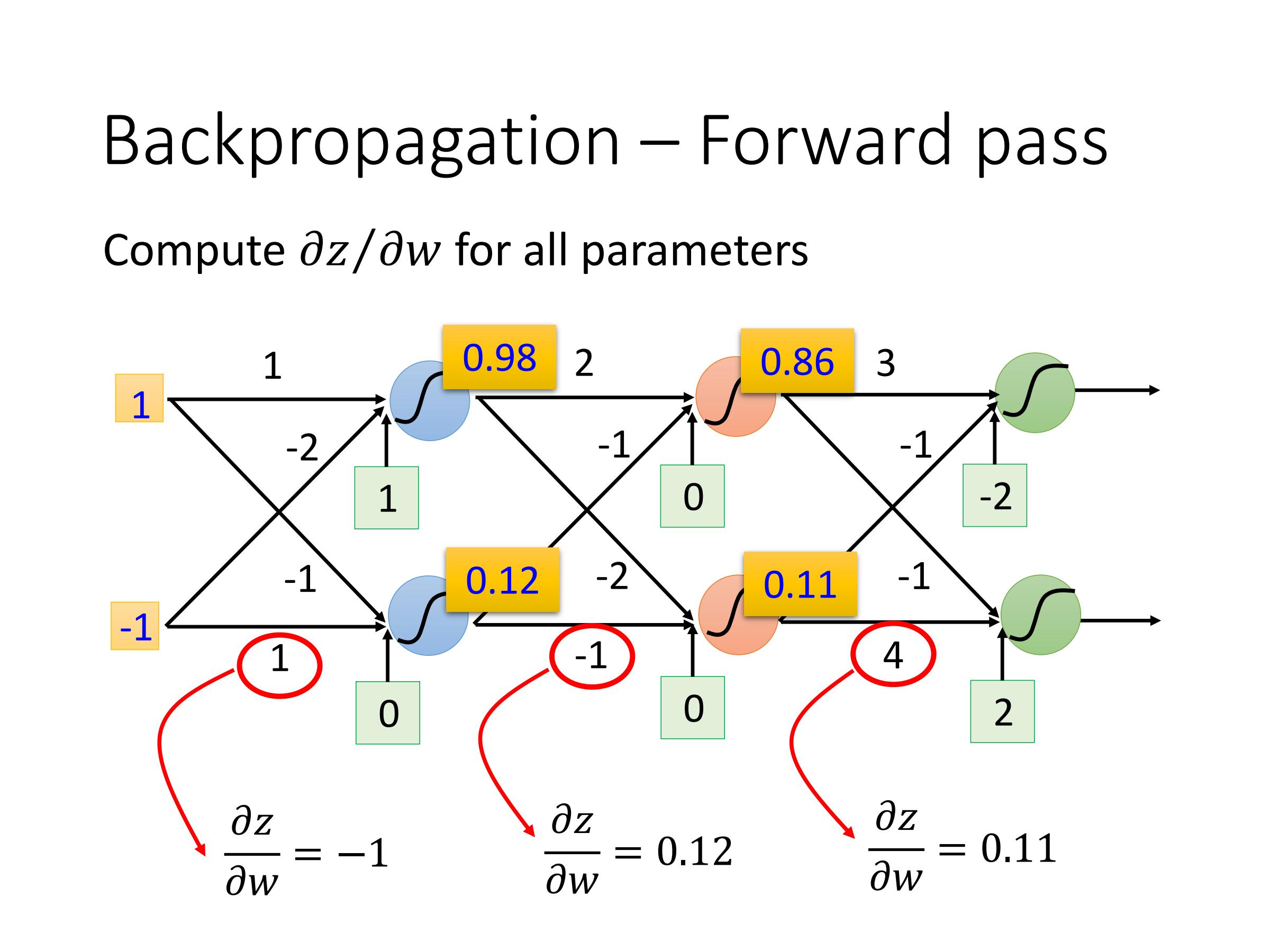
计算：$\frac{\partial z}{\partial w}$——Forward pass

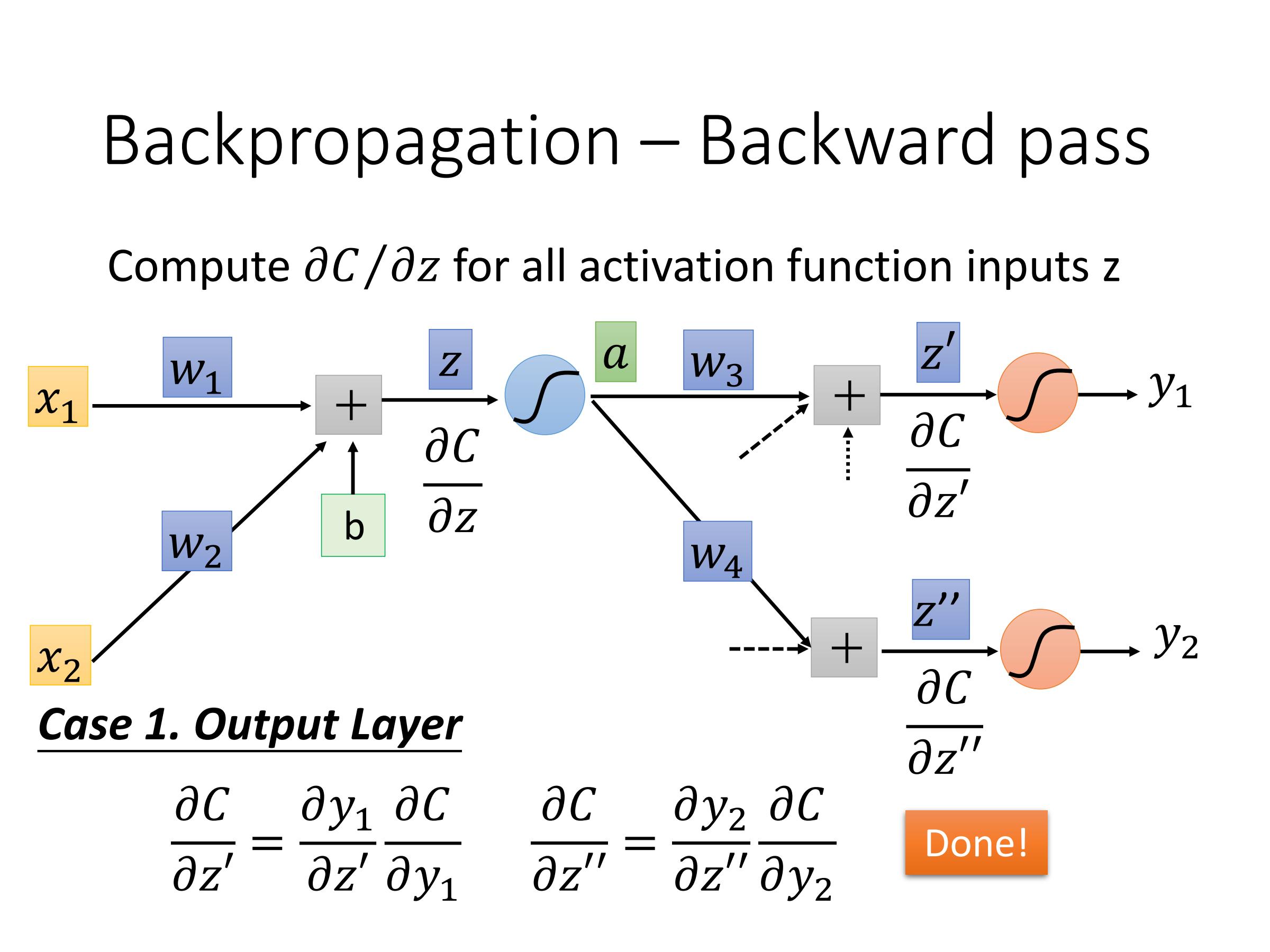
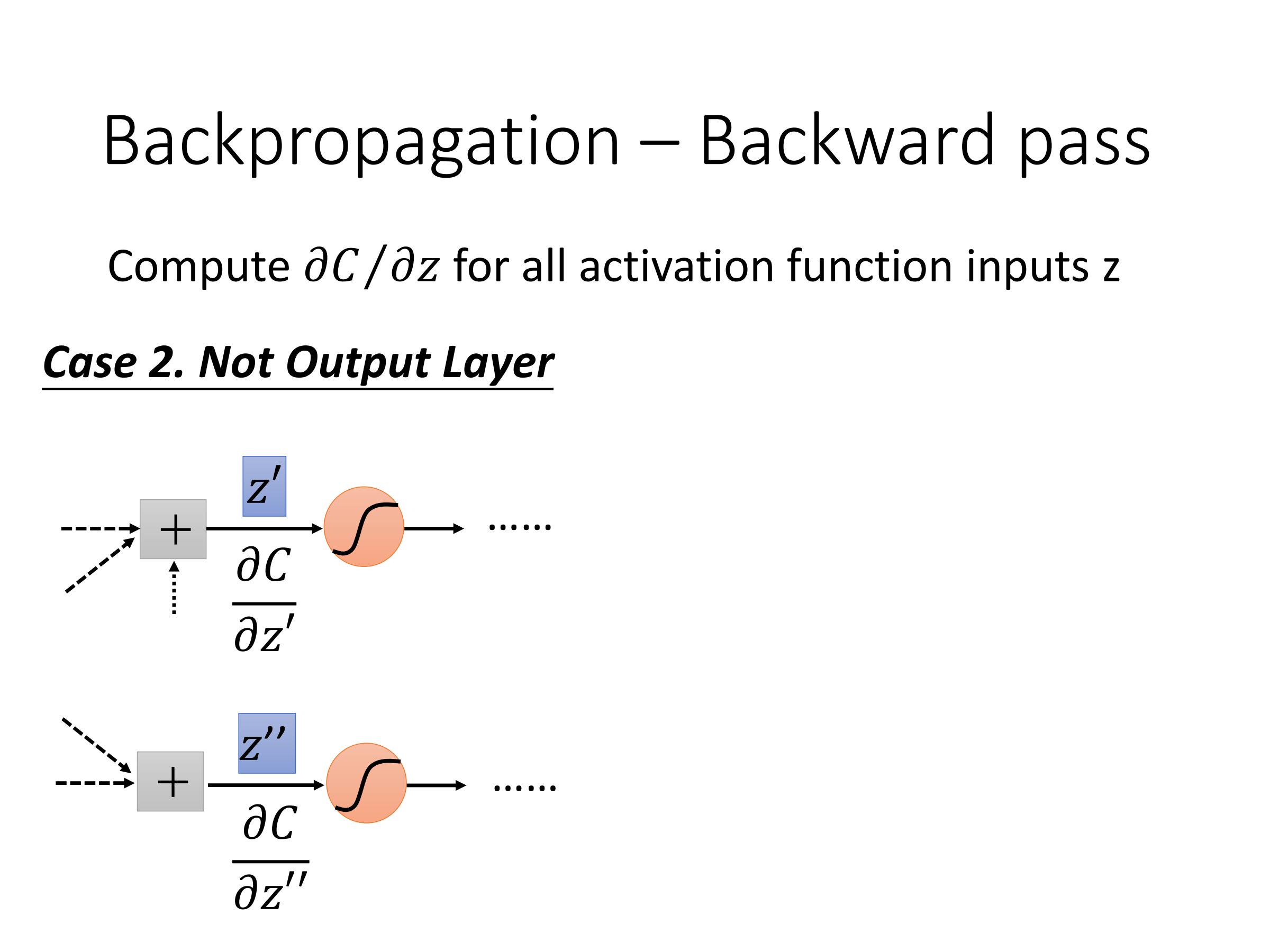
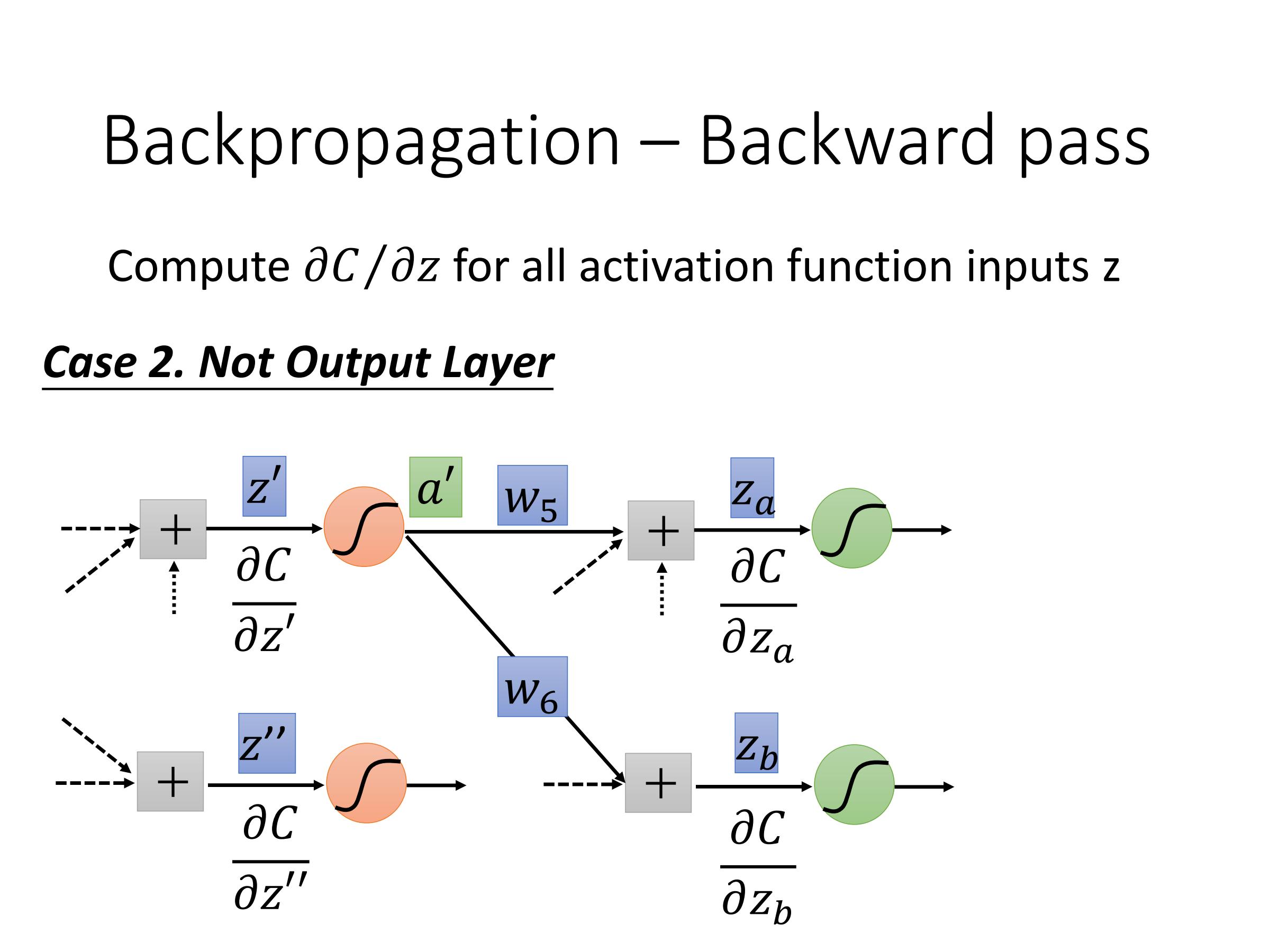
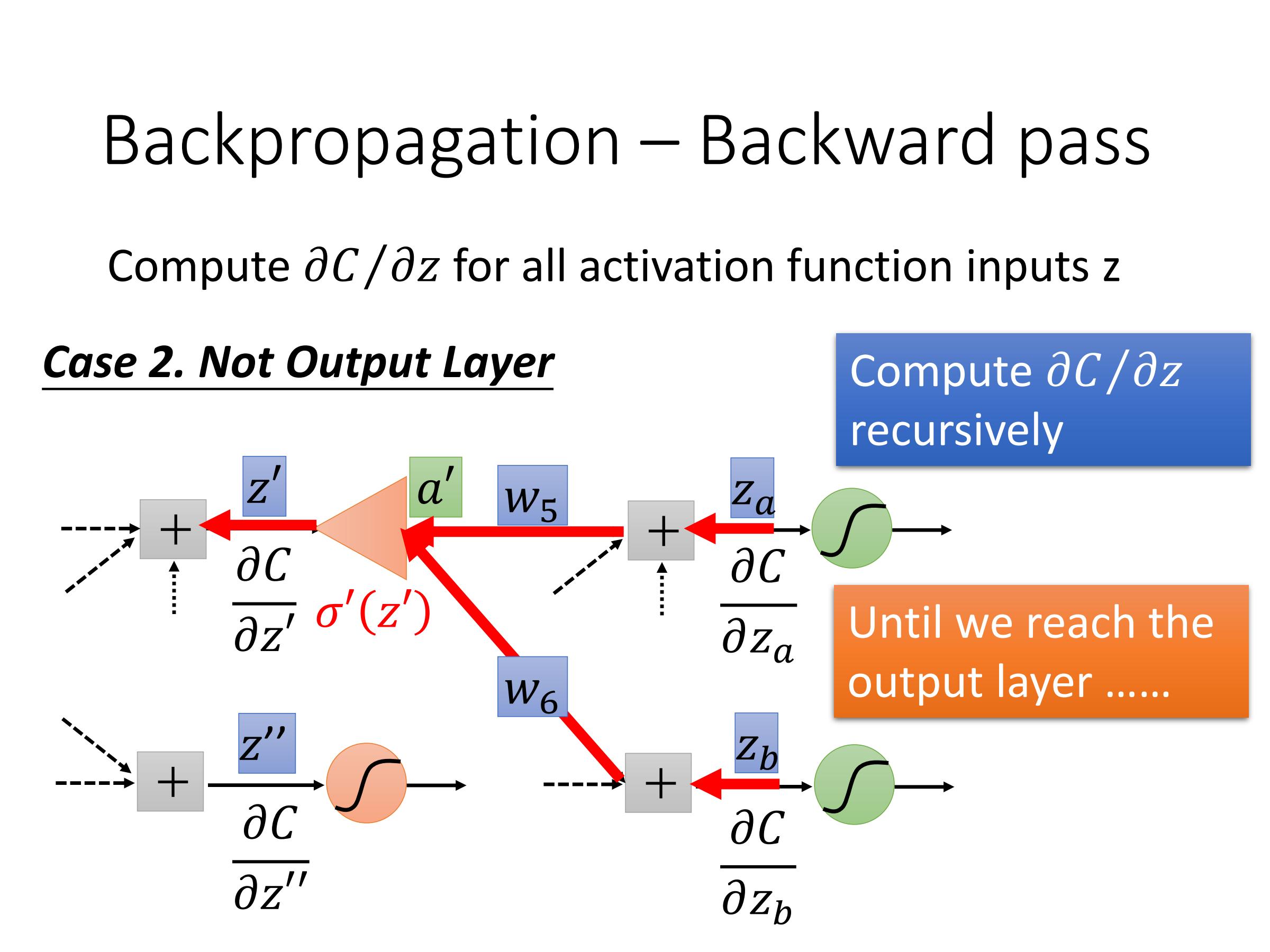
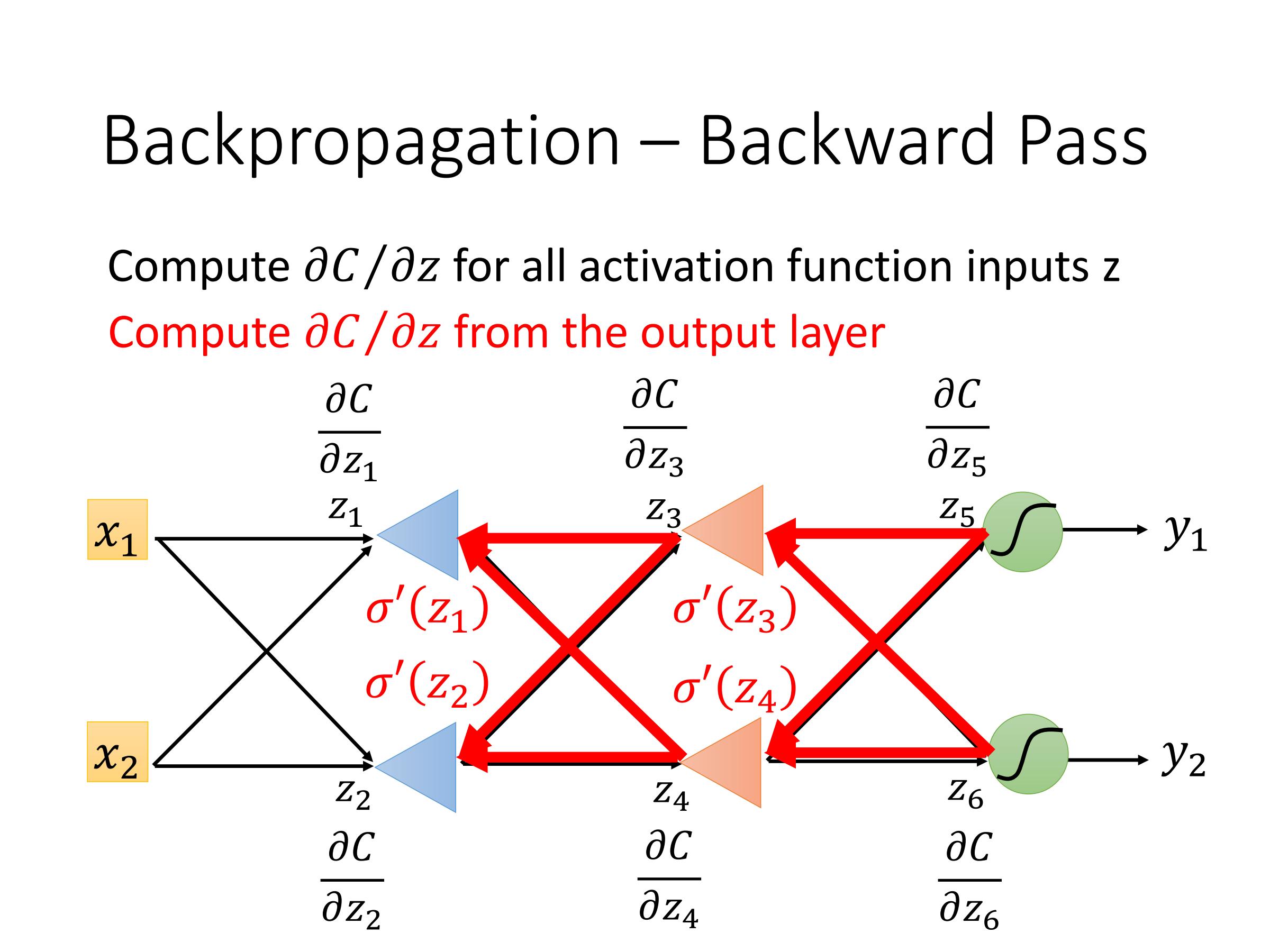
计算：$\frac{\partial C}{\partial z}$——Backward pass

正向传播

反向传播

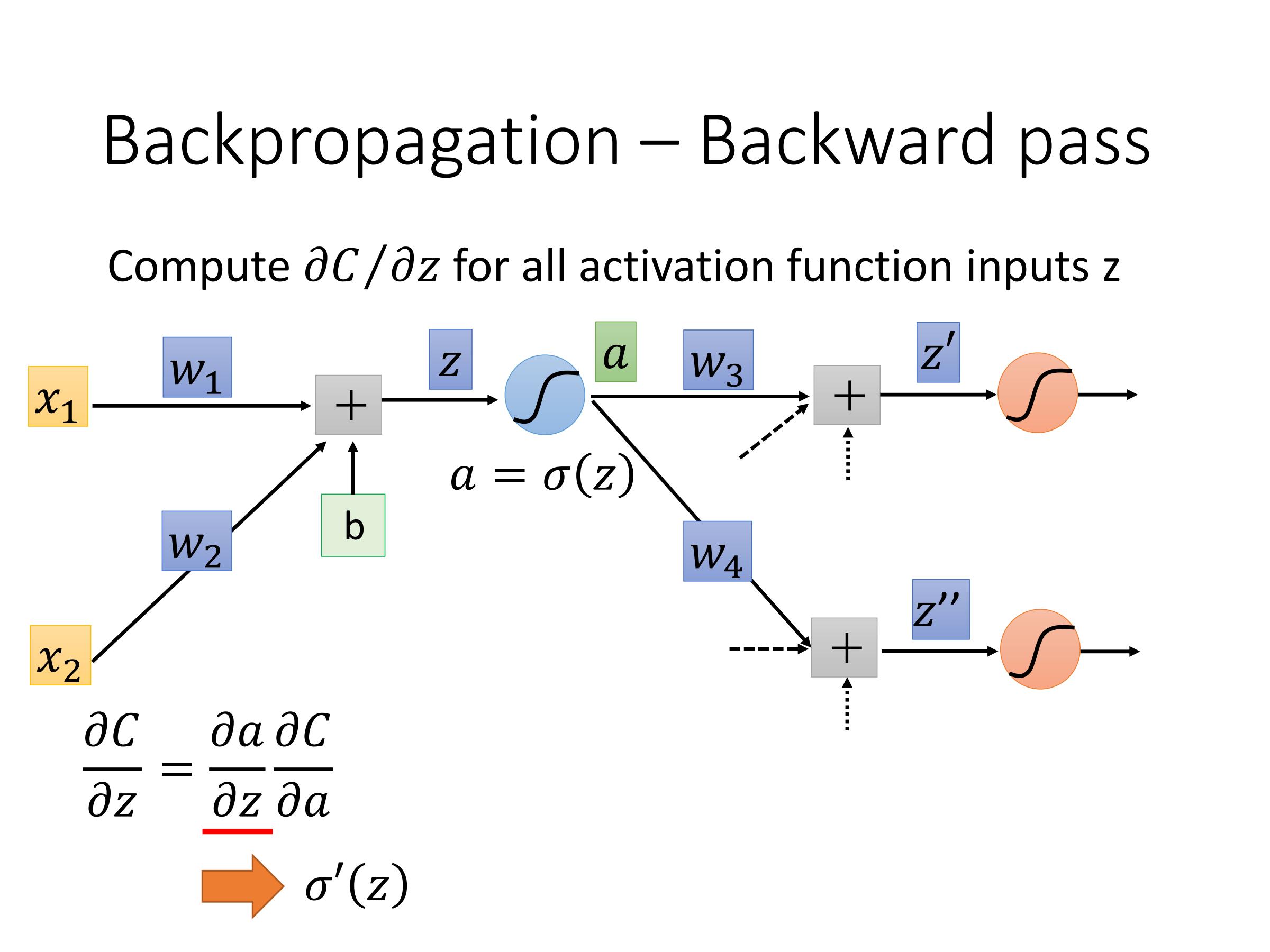
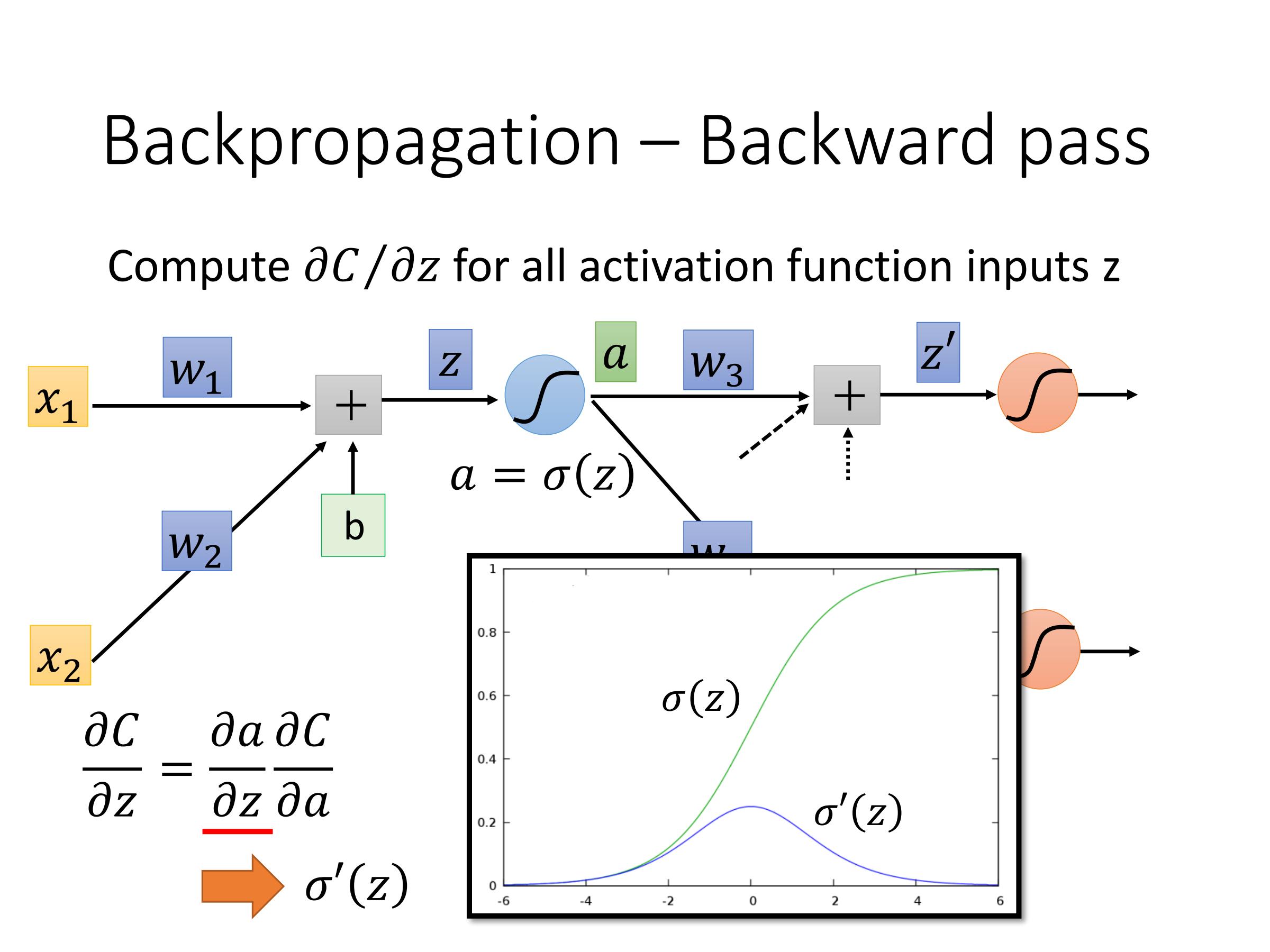
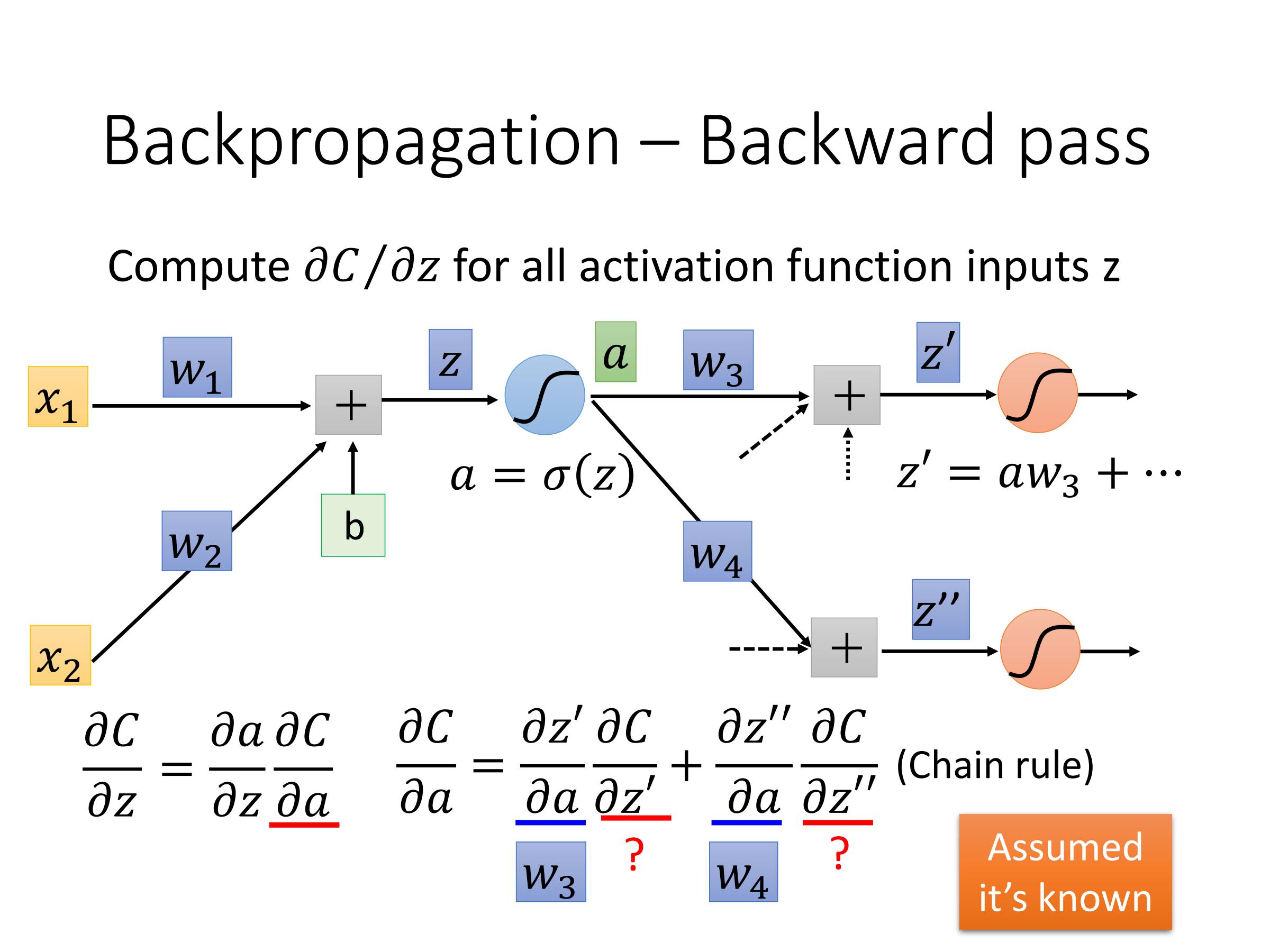
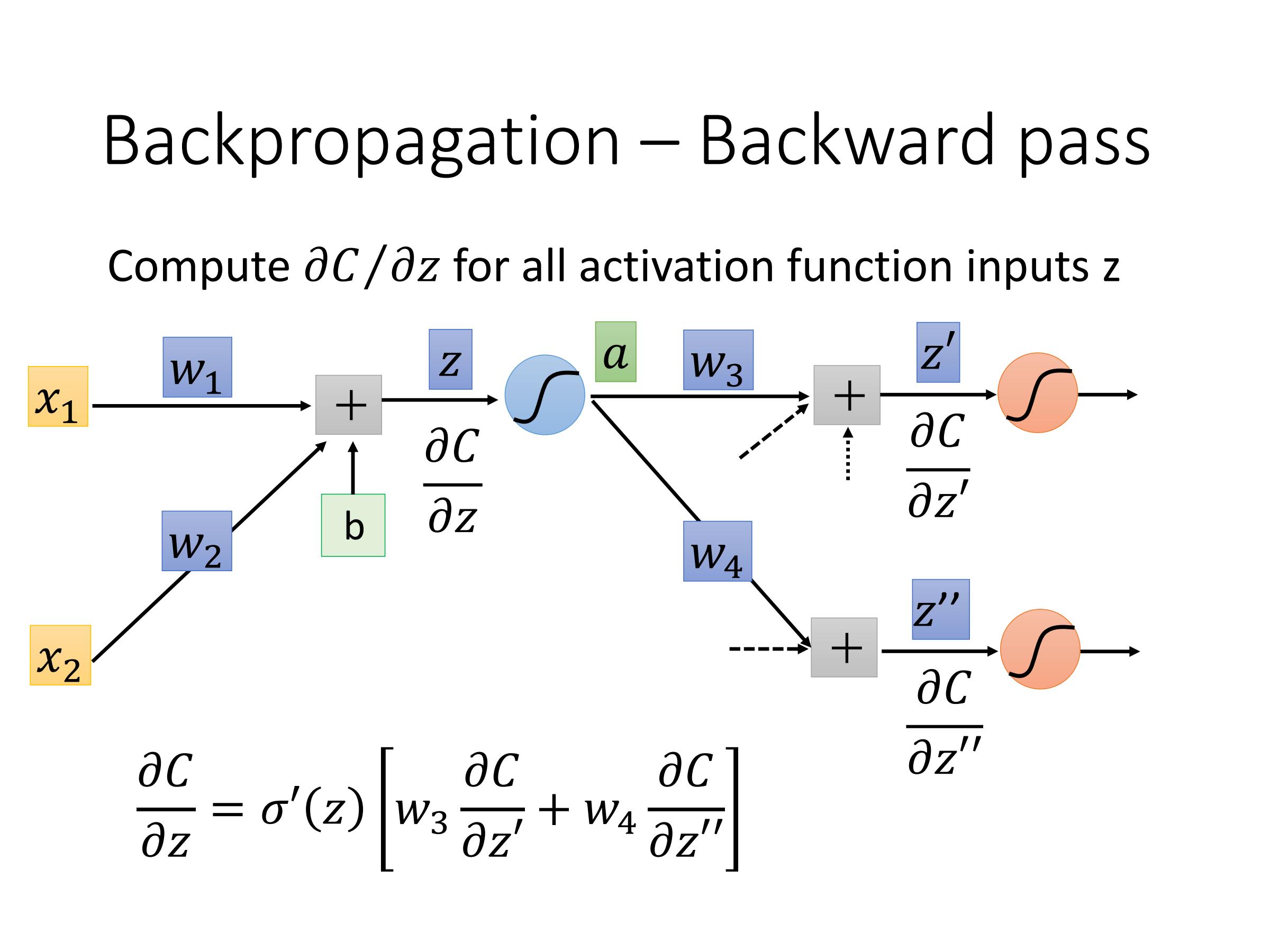
因此，最后问题在于如何计算$\frac{\partial C}{\partial z'}$ 和 $\frac{\partial C}{\partial z''}$

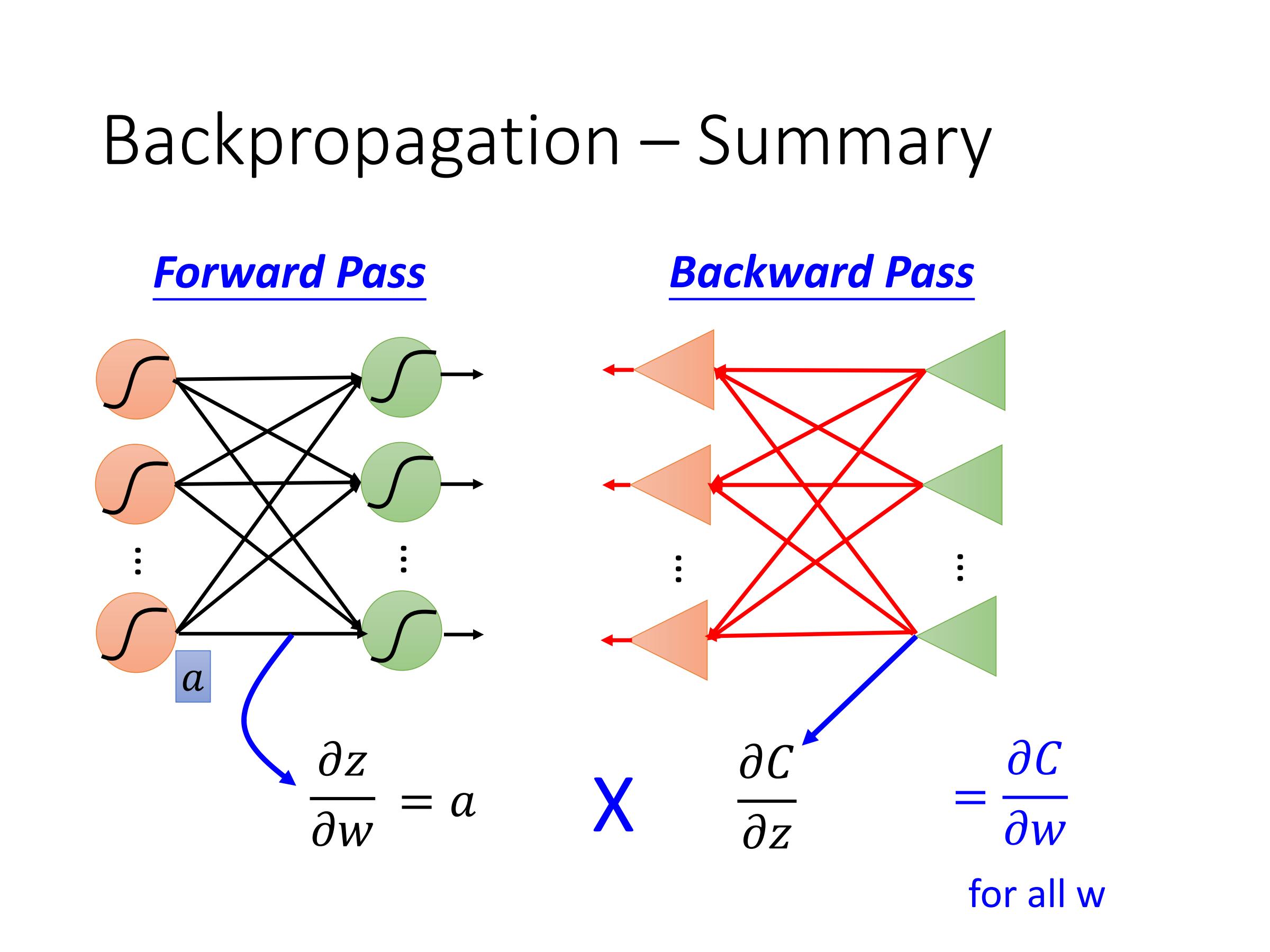
总结

首先，做一个正向传播，算出每个激活函数(activation function)的输出(output)，这个output就是它所连接的weight的$\frac{\partial z}{\partial w}$

在反向传播中，进行反向计算，每一个output就是 $\frac{\partial C}{\partial z}$，$\frac{\partial z}{\partial w} × \frac{\partial C}{\partial z} = \frac{\partial C}{\partial w}$