例:已知宝可梦进化前的数值,通过回归来预测他进化后的数值
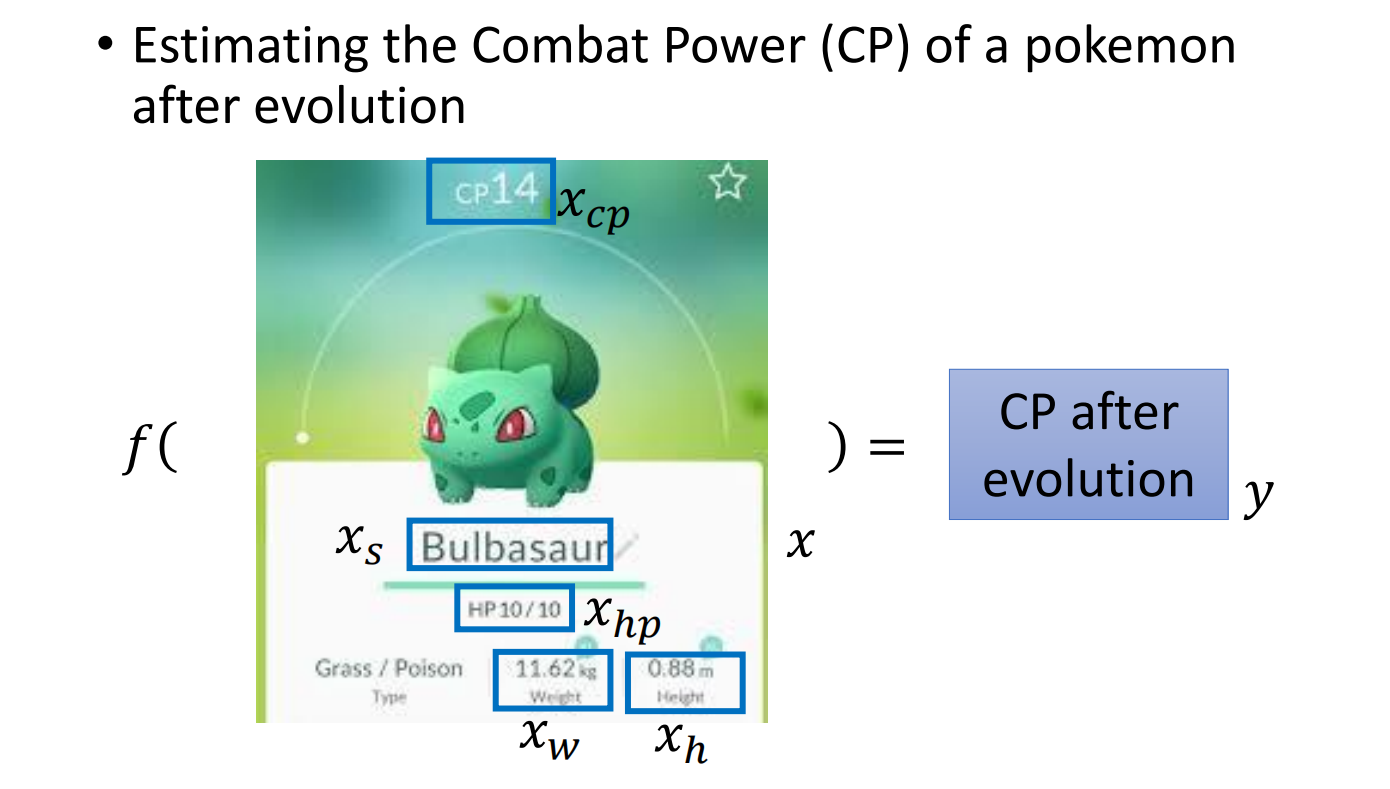
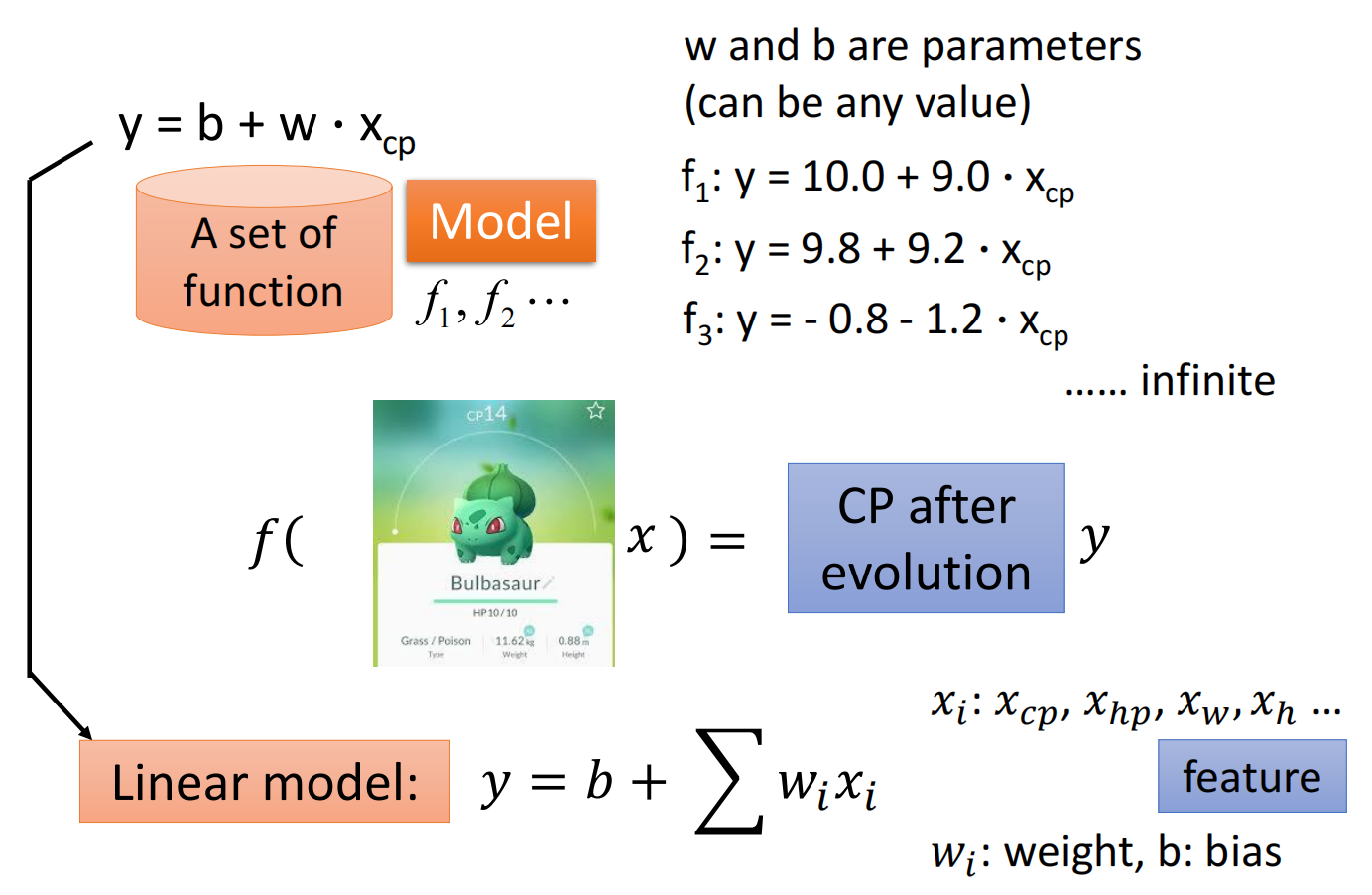
1. Model
定义函数及相关变量,然后构造一个函数集合
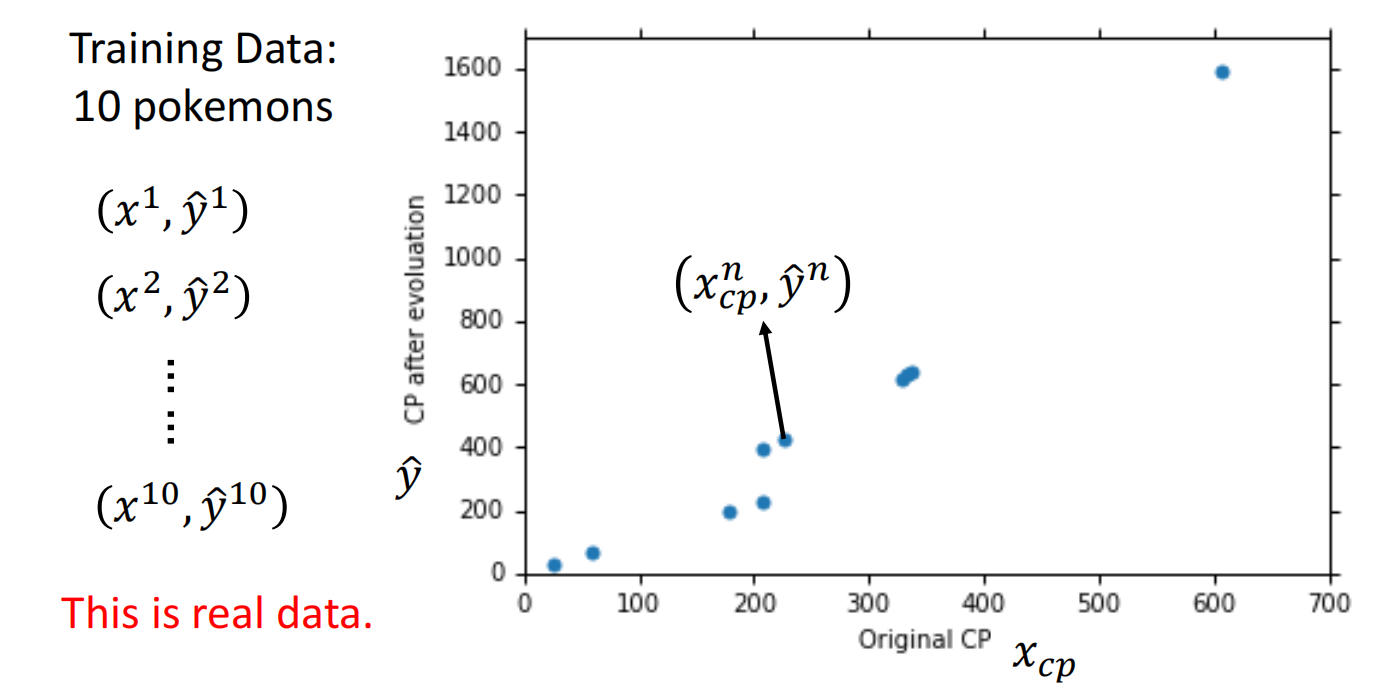
2. Goodness of Function
通过训练集分析函数的好坏
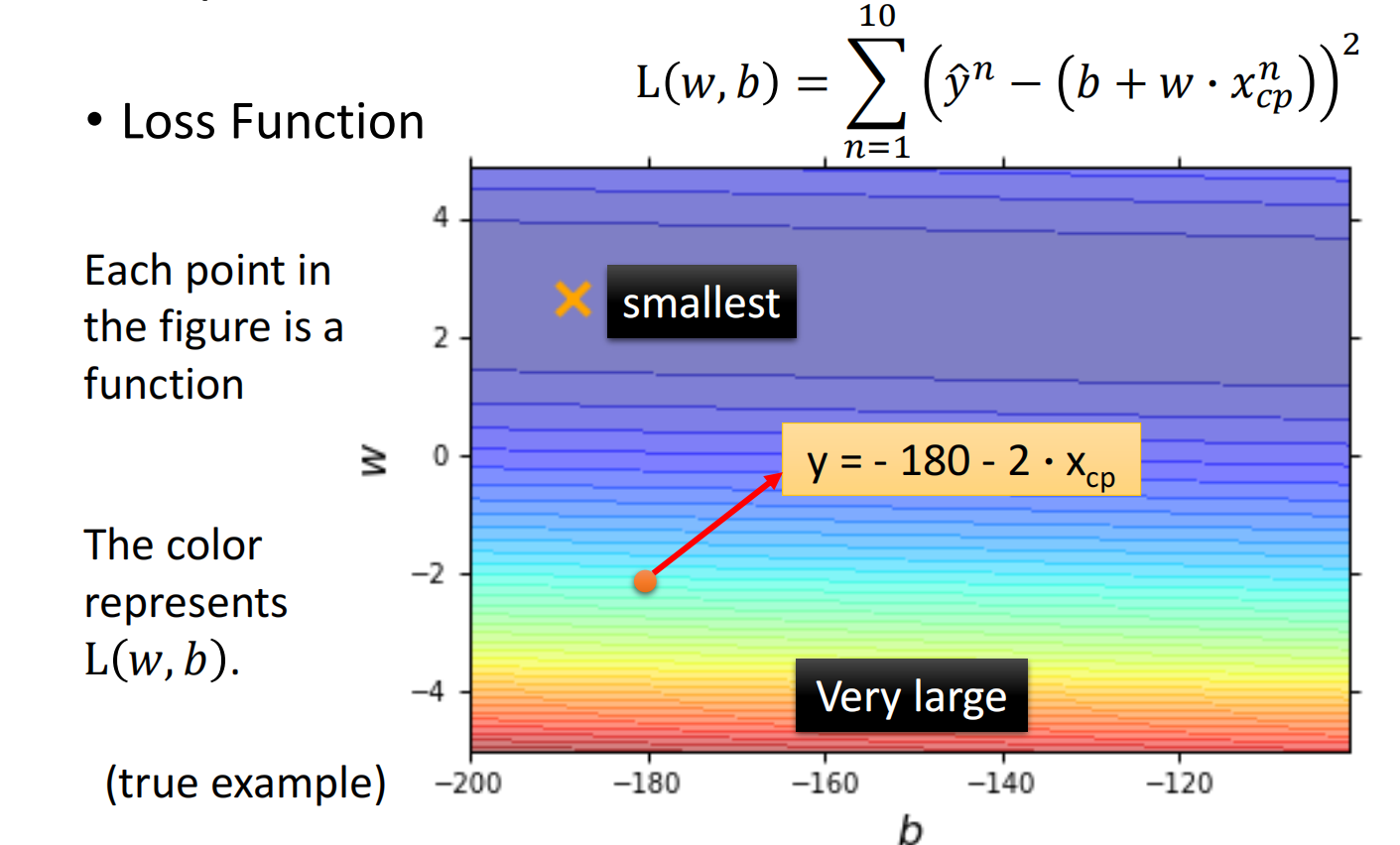
定义一个损失函数 $L$(Loss Function),输入为function,输出为好坏:$L(f) = L(w,b)$,即损失函数是在衡量一组参数的好坏
这里使用 $方差*num$ 来作为损失函数
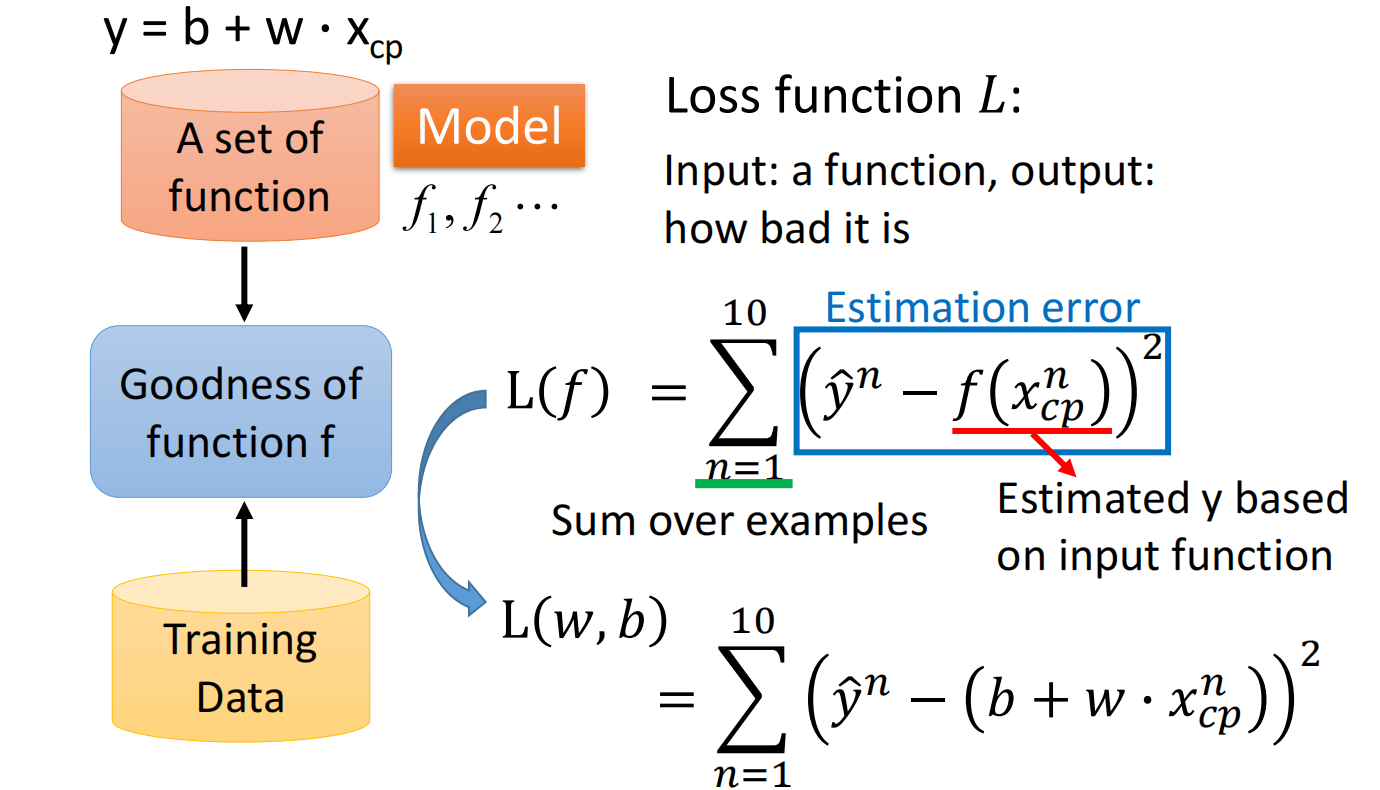
损失函数如下:
3. Best Function
从函数集合中挑出最好的函数:
找 $f$ 使得 $L(f)$ z值最小: $f^{*}=\arg \min _{f} L(f)$
或者说,找到合适的 $w$ 和 $b$, 使得 $L(w,b)$ 最小:$w^{*}, b^{*}=\arg \min _{w, b} L (w, b)=\arg \min _{w, b} \sum_{n=1}^{10}\left(\hat{y}^{n}-\left(b+w \cdot x_{c p}^{n}\right)\right)^{2}$
可以通过梯度下降来寻找最优解
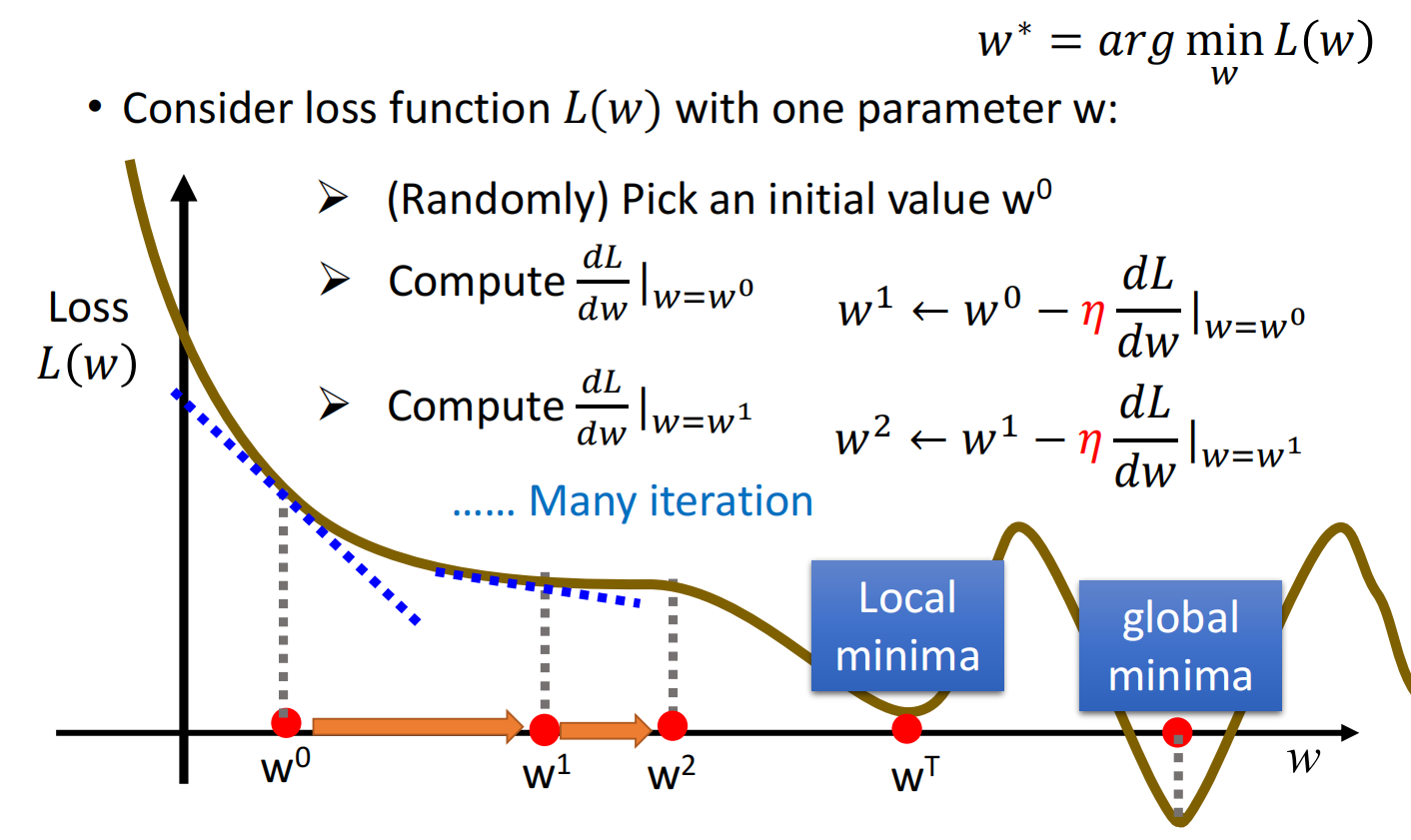
梯度下降 (Gradient Descent)
- 仅有一个参数的情况下
假设考虑带有参数 $w$ 的损失函数 $L(w)$ :
- 随机 (或其他) 选取一个初始点 $w_0$
- 计算 $w$ 对 损失函数的微分 $\left.\frac{d L}{d w}\right|_{w=w^{0}}$,根据微分调整 $w$ 的值
- 每一步的step size为:$-\left.\eta \frac{d L}{d w}\right|_{w=w^{0}}$,其中 $\eta$ 为learing rate
- 一直移动直到找到局部最小值,此时微分为0
- 两个参数的情况下
$$\nabla L=\left[\begin{array}{l}
\frac{\partial L}{\partial w} \\
\frac{\partial L}{\partial b}
\end{array}\right]_{\text {gradient }} $$

4. Results
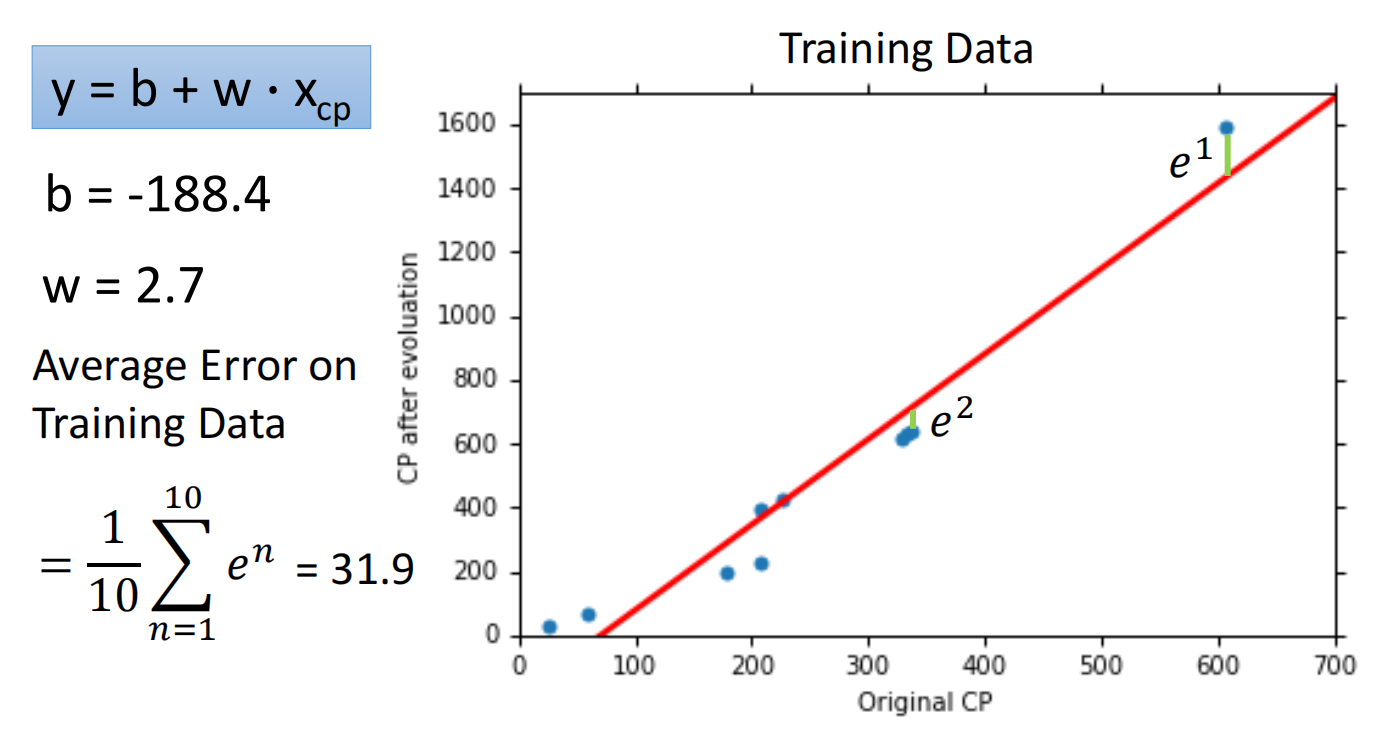
可以使用测试集测试效果
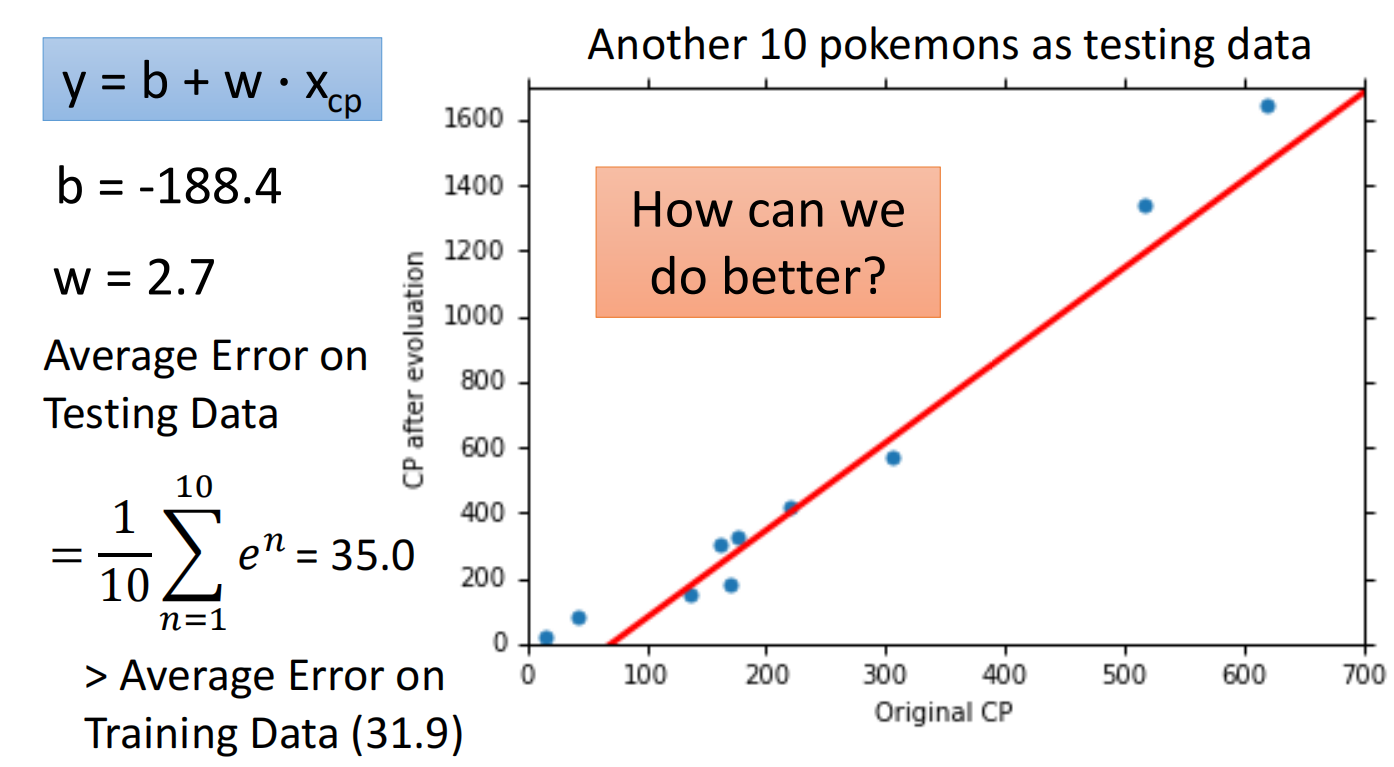
可以重新设计model,寻求更优解
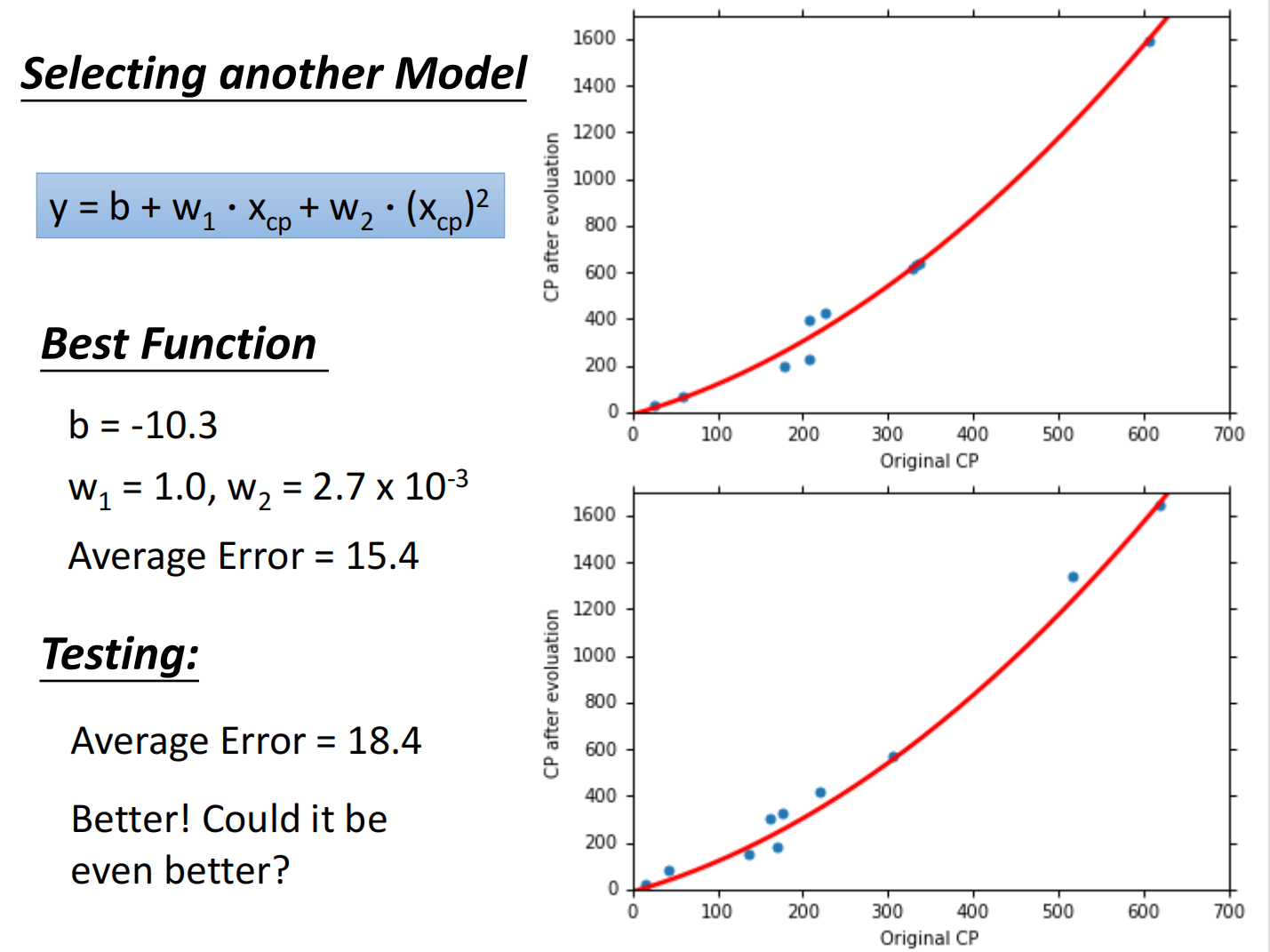
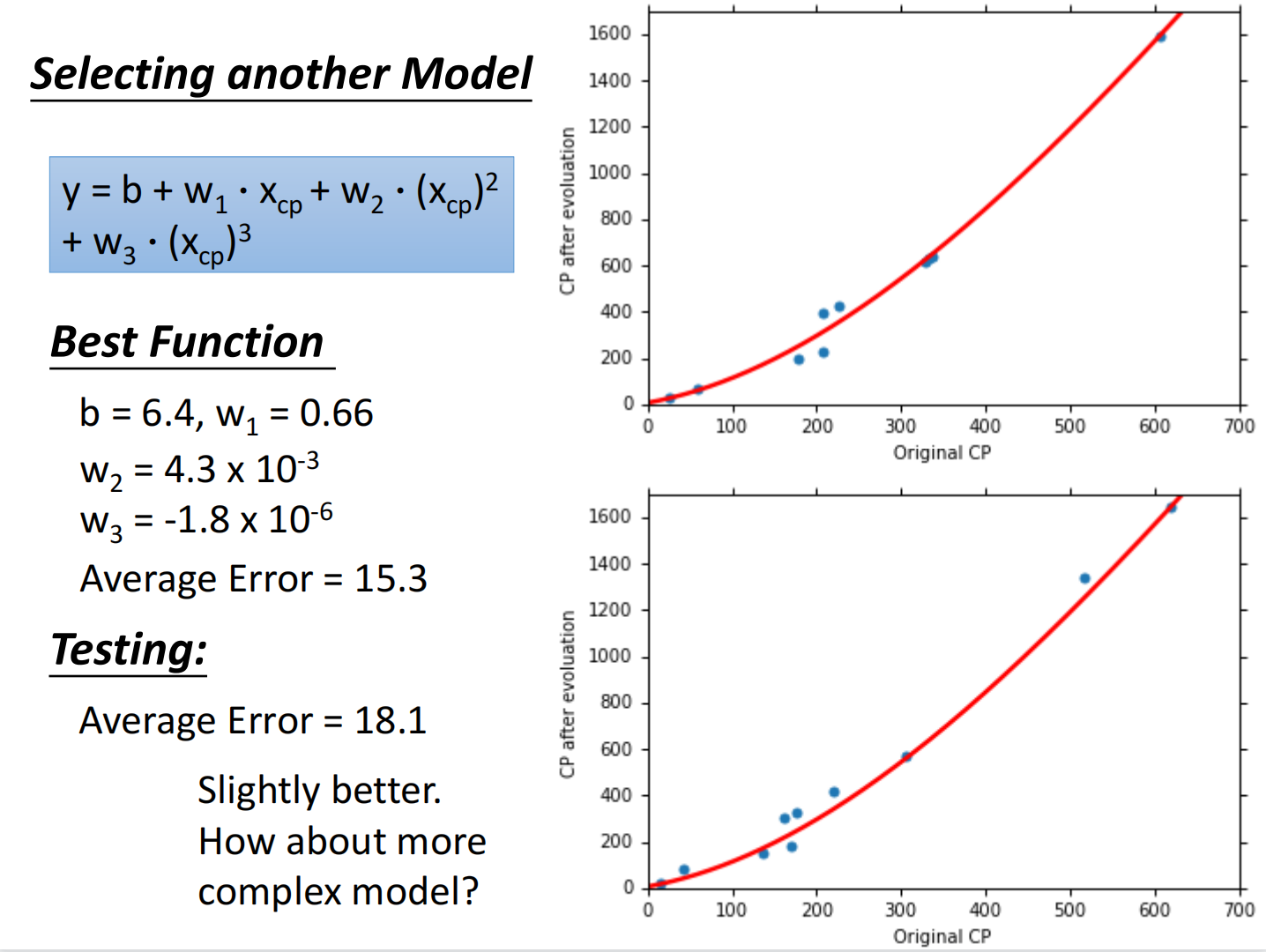
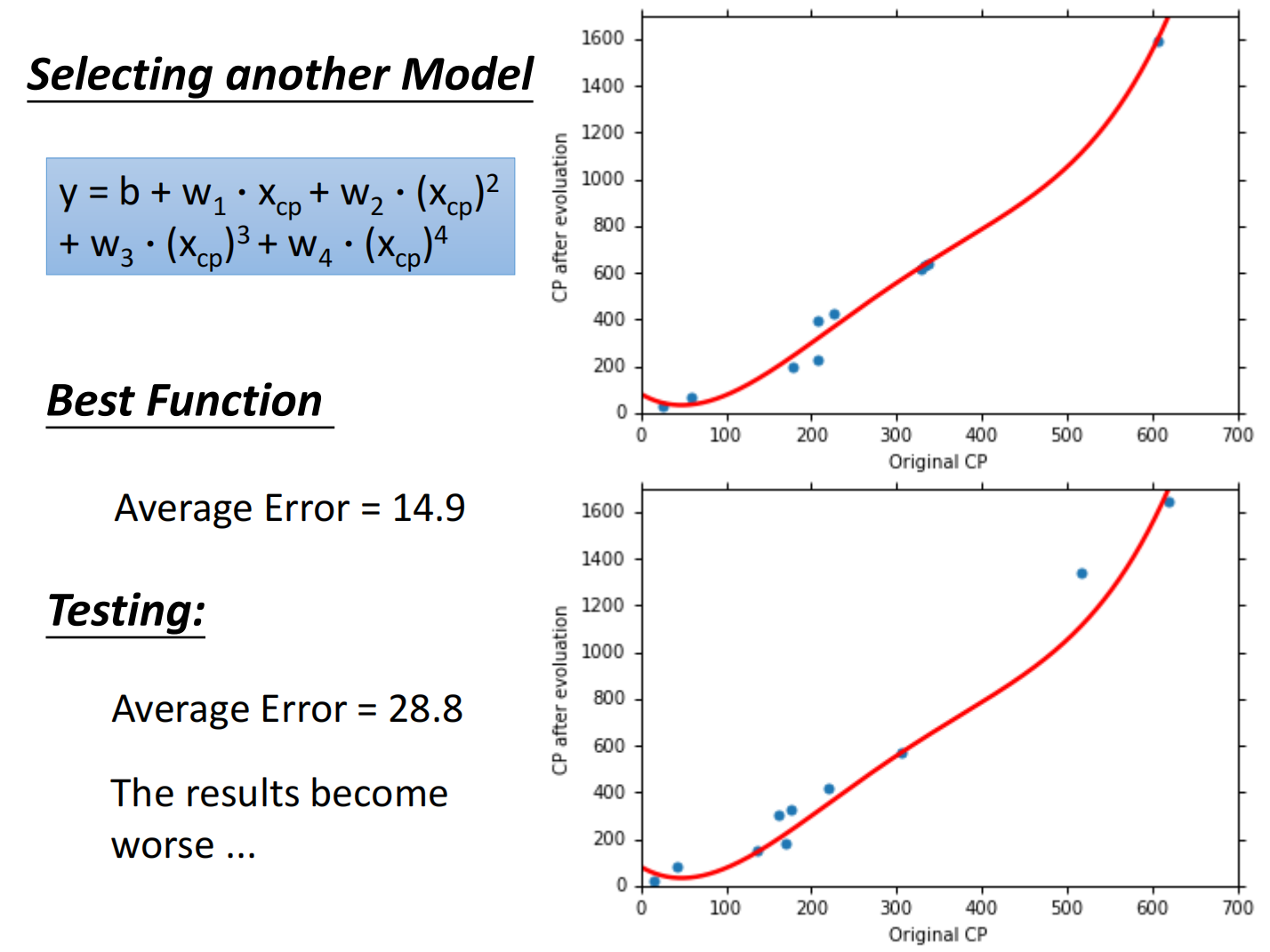
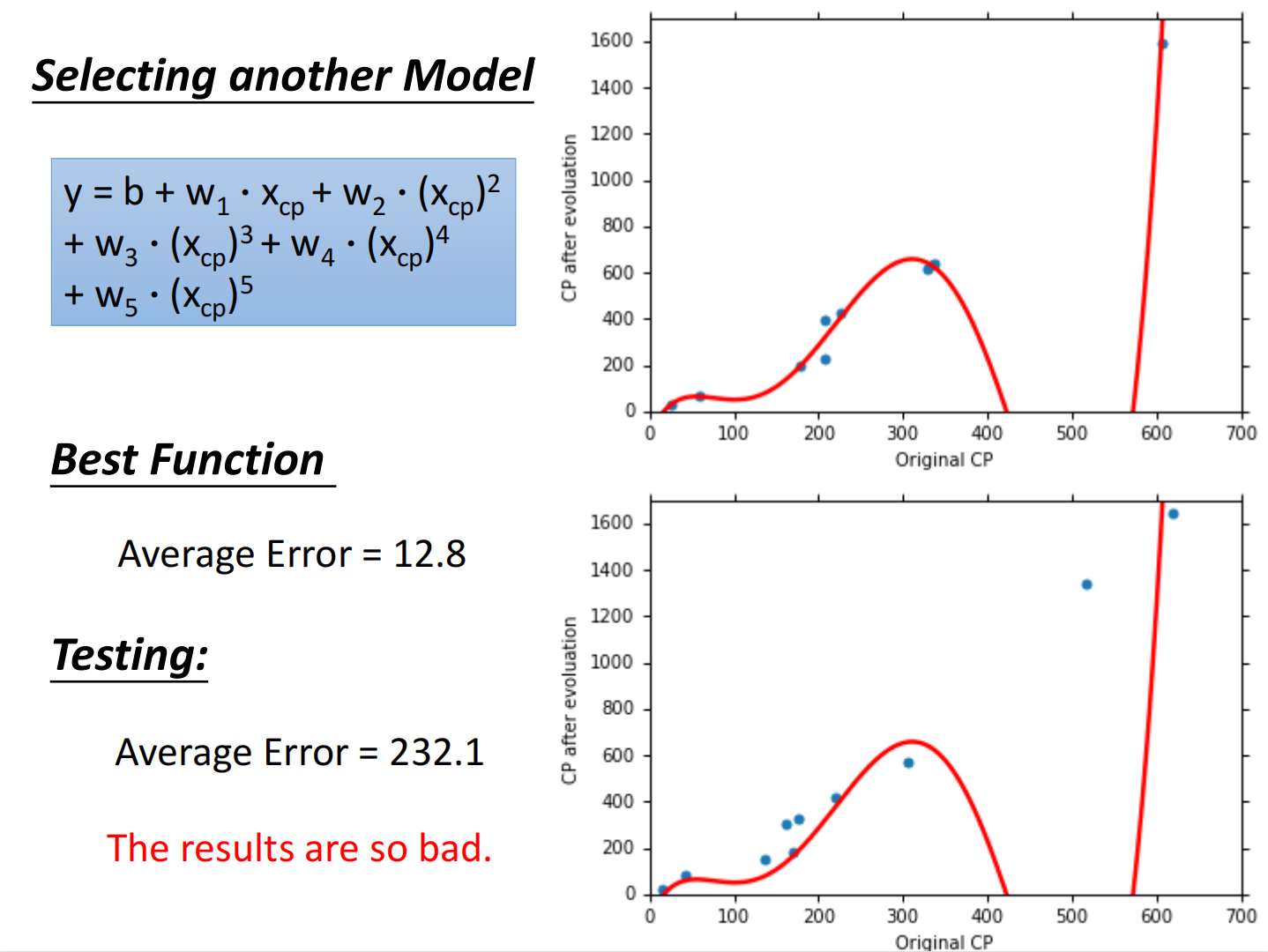
总结如下:
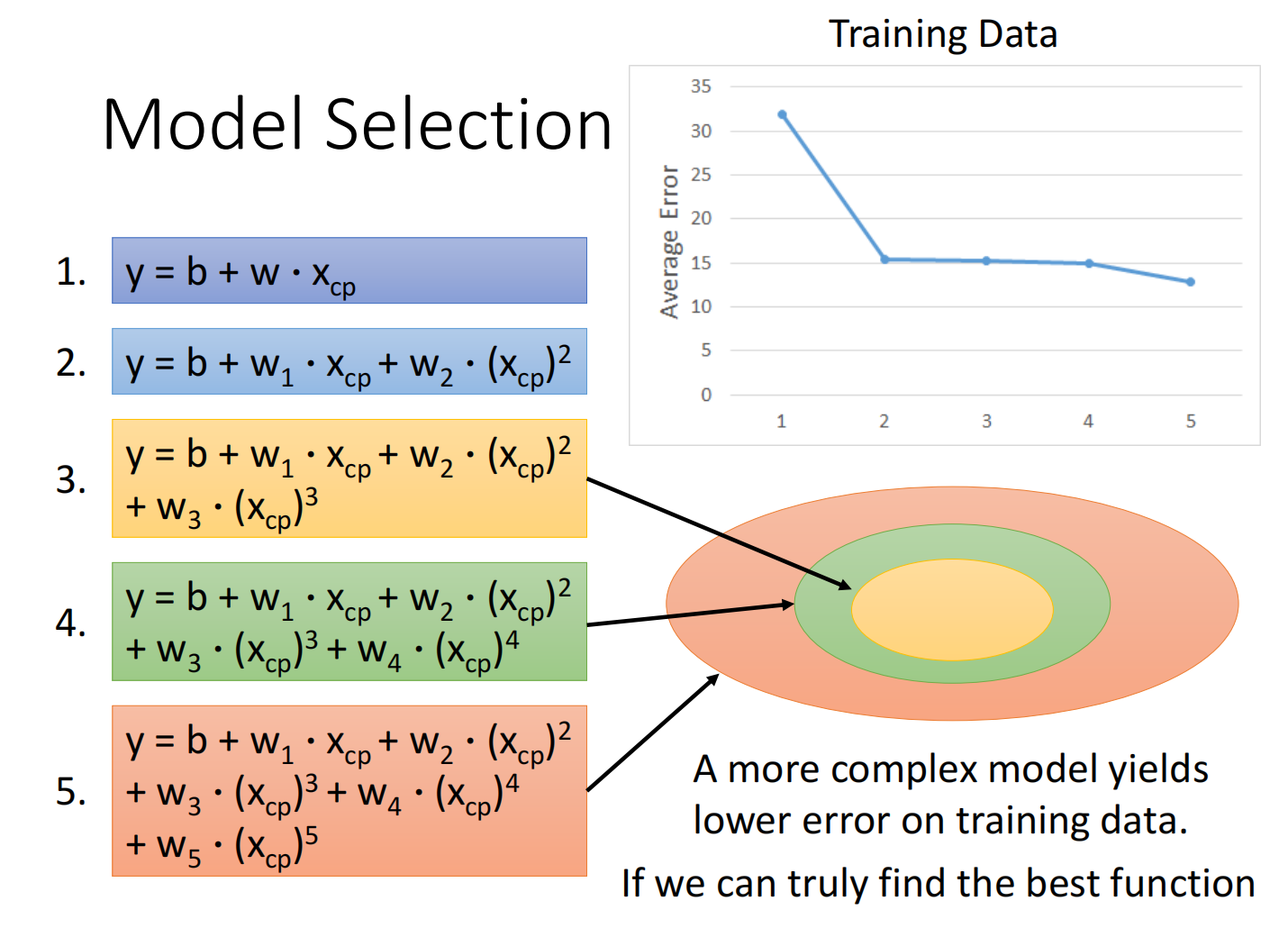
但在测试集上,当函数复杂度过高的时候反而效果不好,称之为过拟合(Overfitting)

5. more data
数据集越大越好找function
当数据增多时,我们可以发现分类
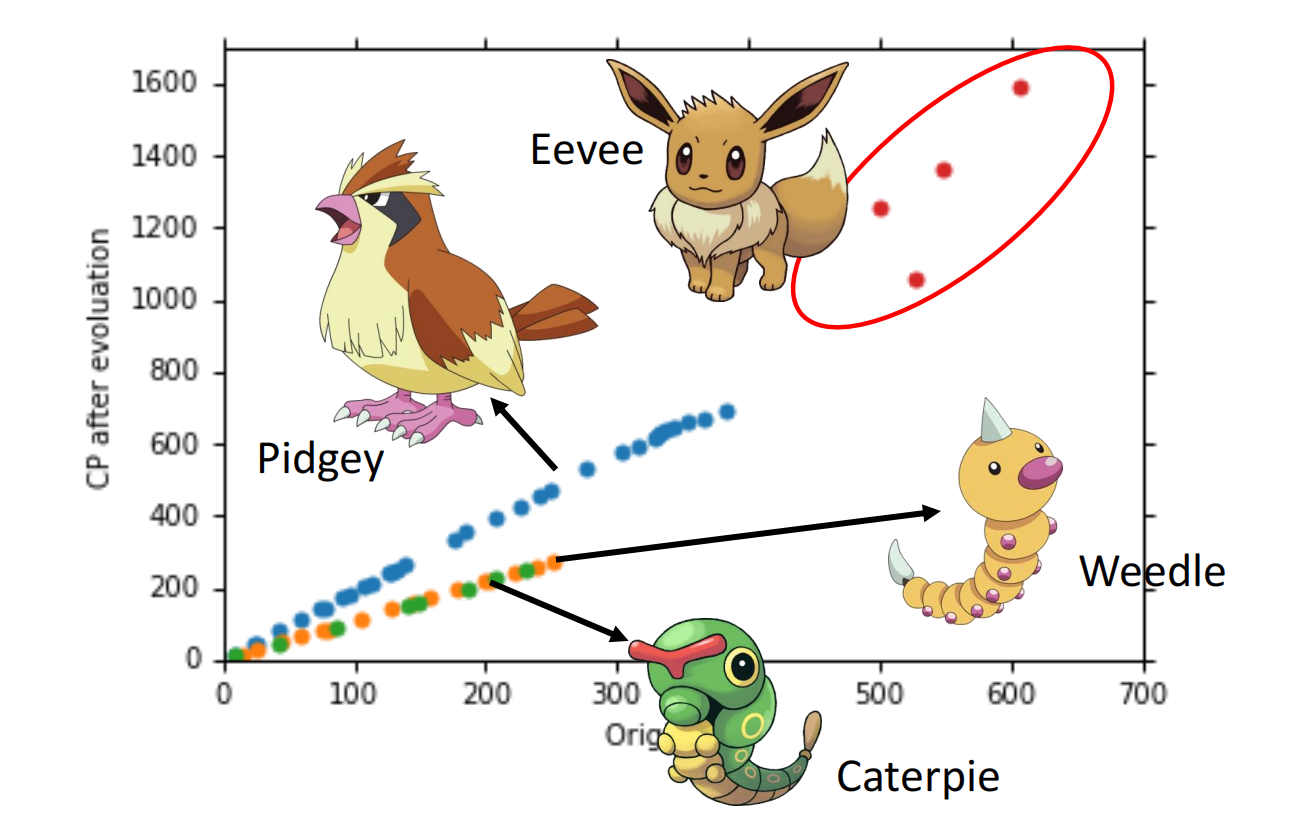
重新设计model:
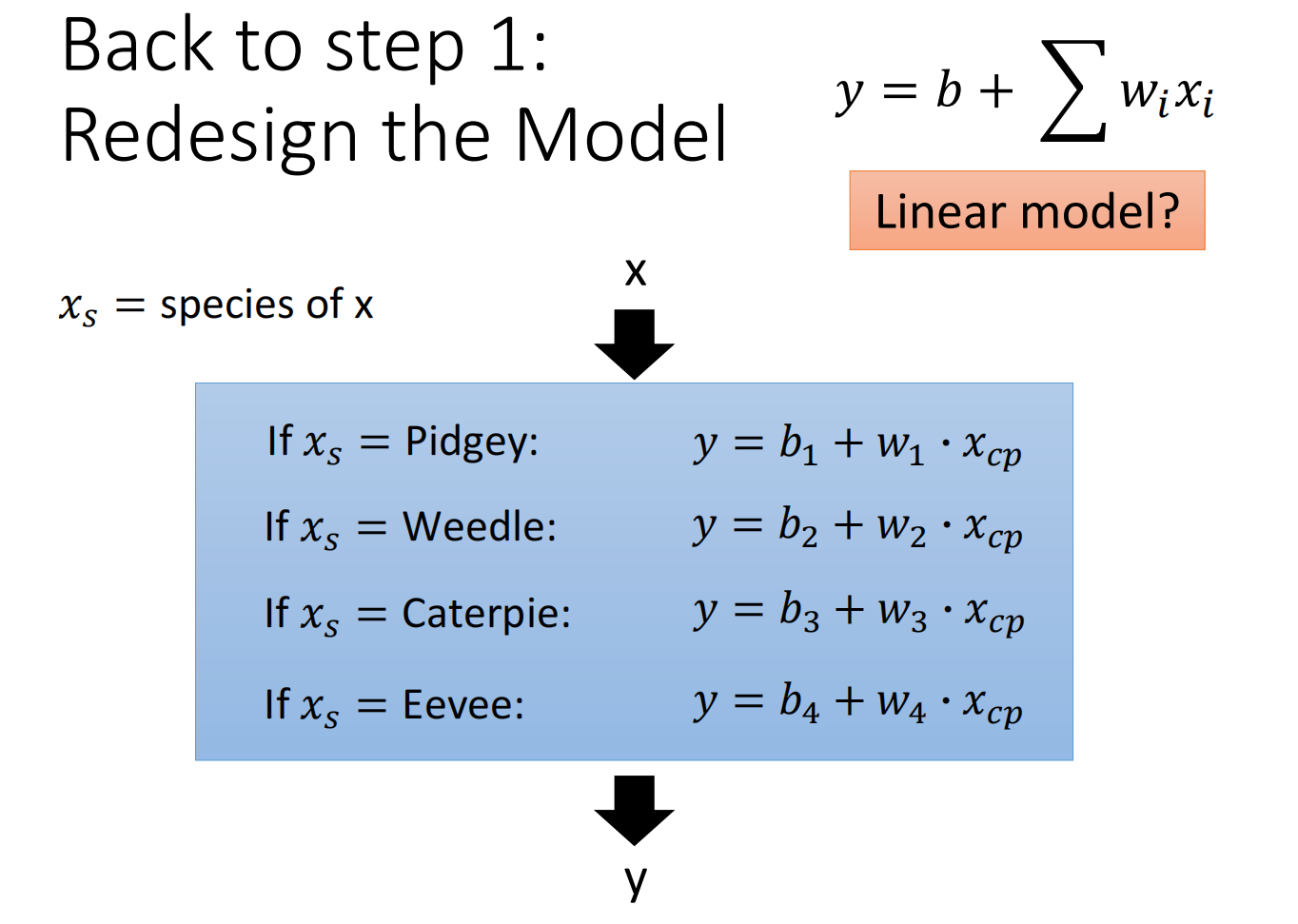

当分类后,我们发现效果会更好:
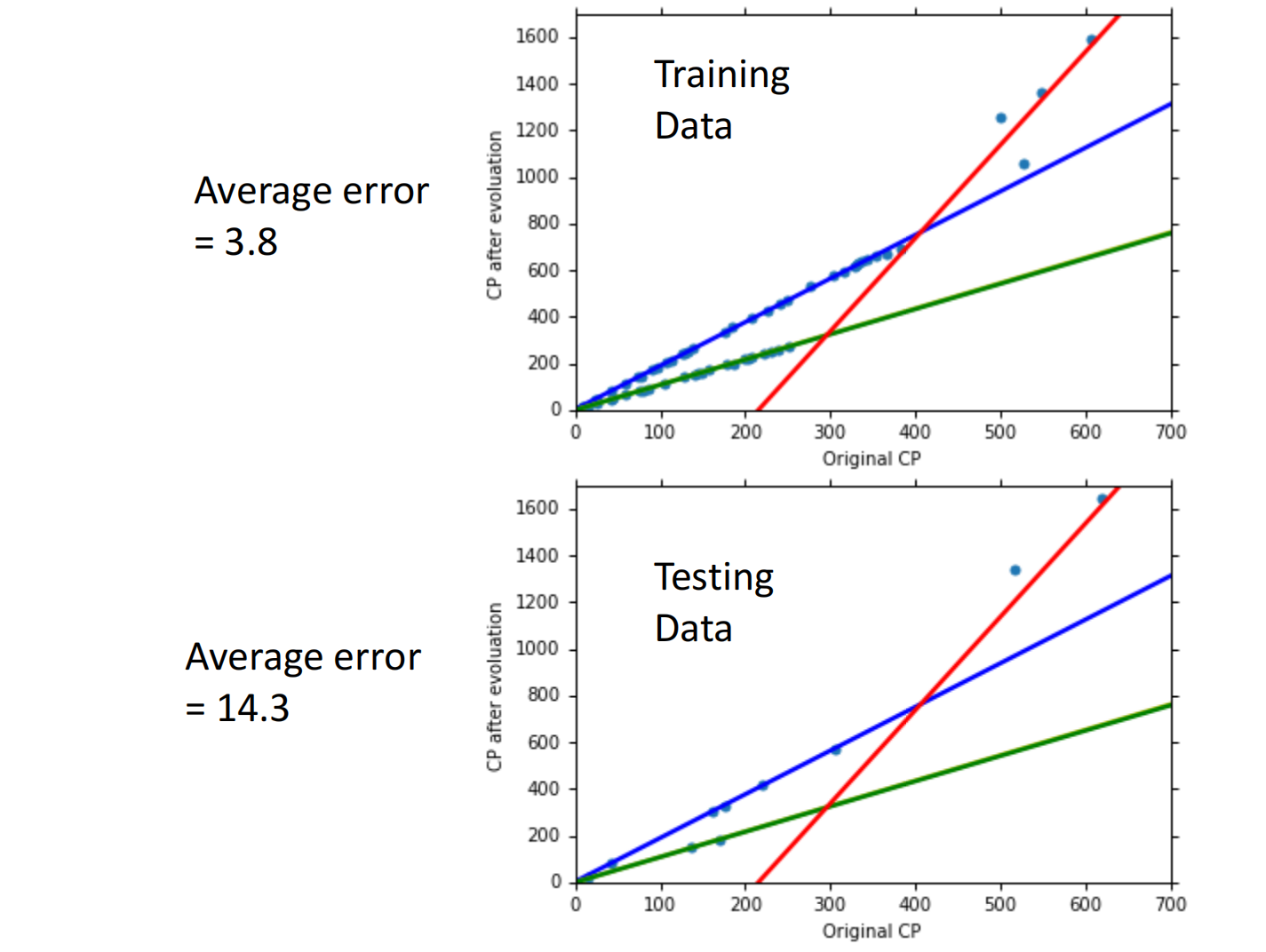
但还有离群点,我们可以考虑是否存在其他的因素
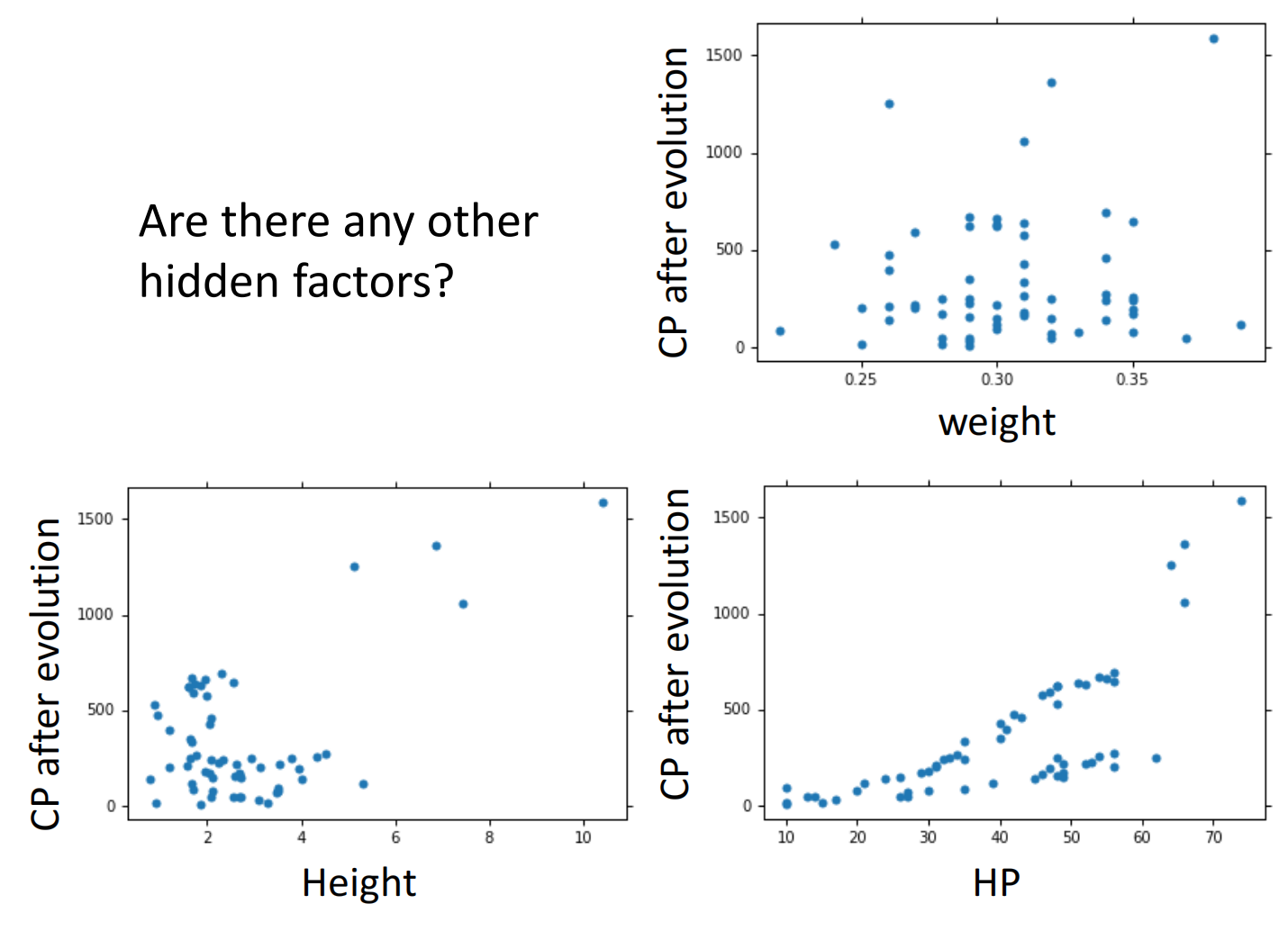
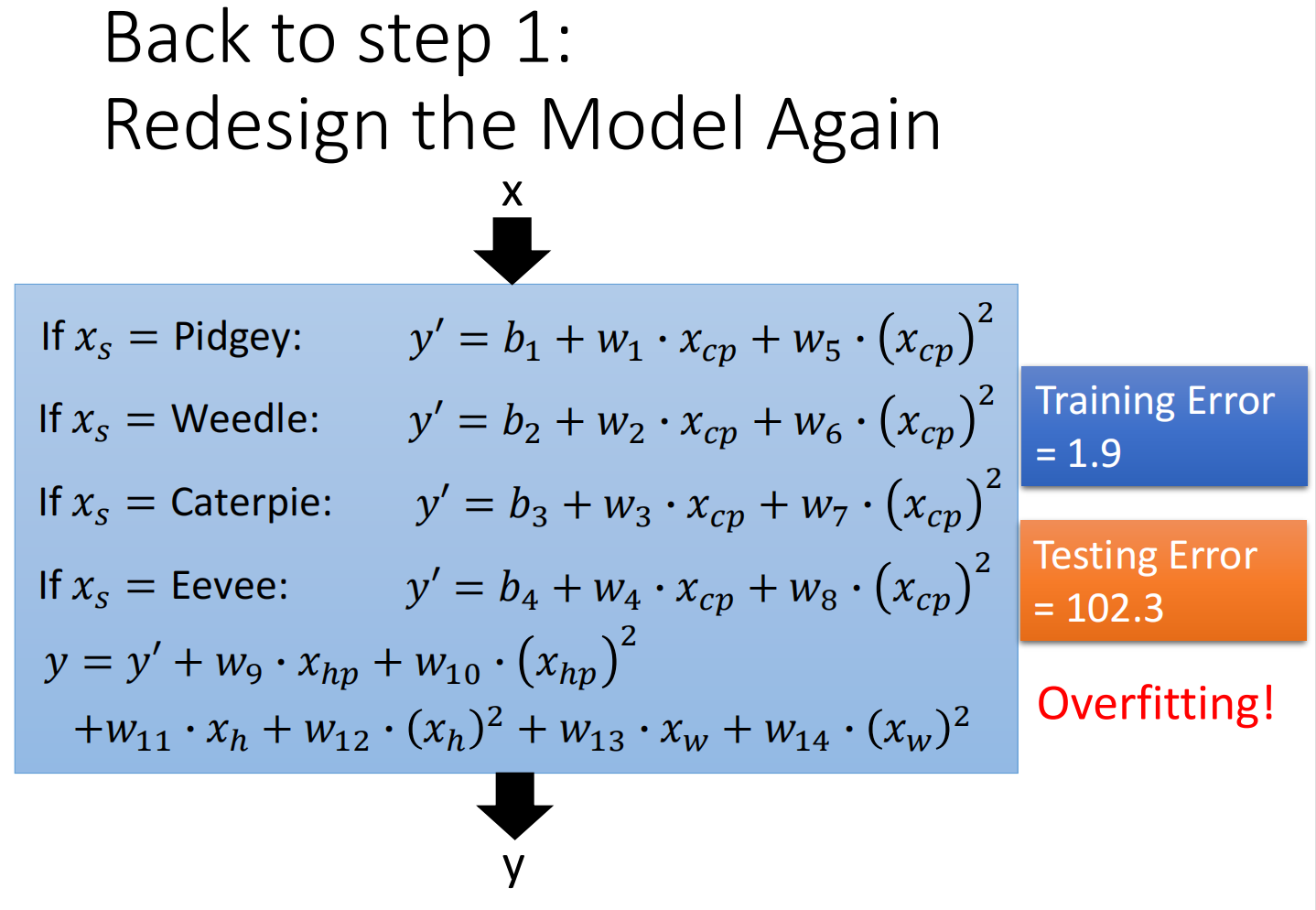
因此再次重新设计model,把所有可能因素全部加入,发现会过拟合:
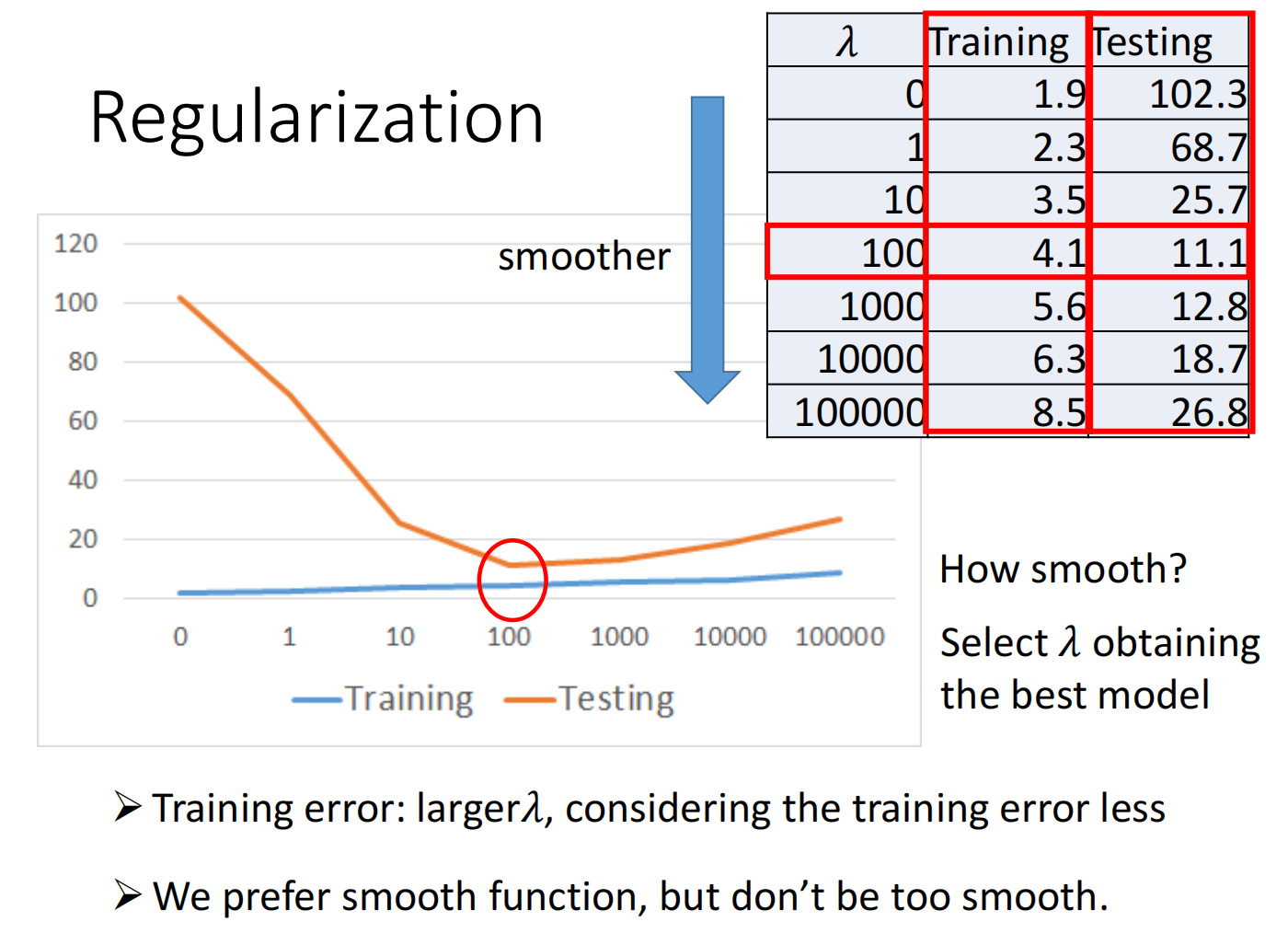
因此我们可以使用正则化(regularization):
在损失函数中加入一个关于$w$的式子$\lambda \sum\left(w_{i}\right)^{2}$,使得变化更加平滑
不加入参数$bisa$是因为只影响上下值,不影响变化率