寻找一个函数，输入为 $x$，输出为 $x$ 的类别

今天介绍的是一种概率生成模型的分类方法
例：根据宝可梦某些数值对它的系别进行分类

分类与回归

值得注意的是，分类问题不能使用回归去硬解
比如在这里我们使用回归去解决二元分类问题，在回归问题中，我们希望蓝色越接近1越好，红色越接近-1越好

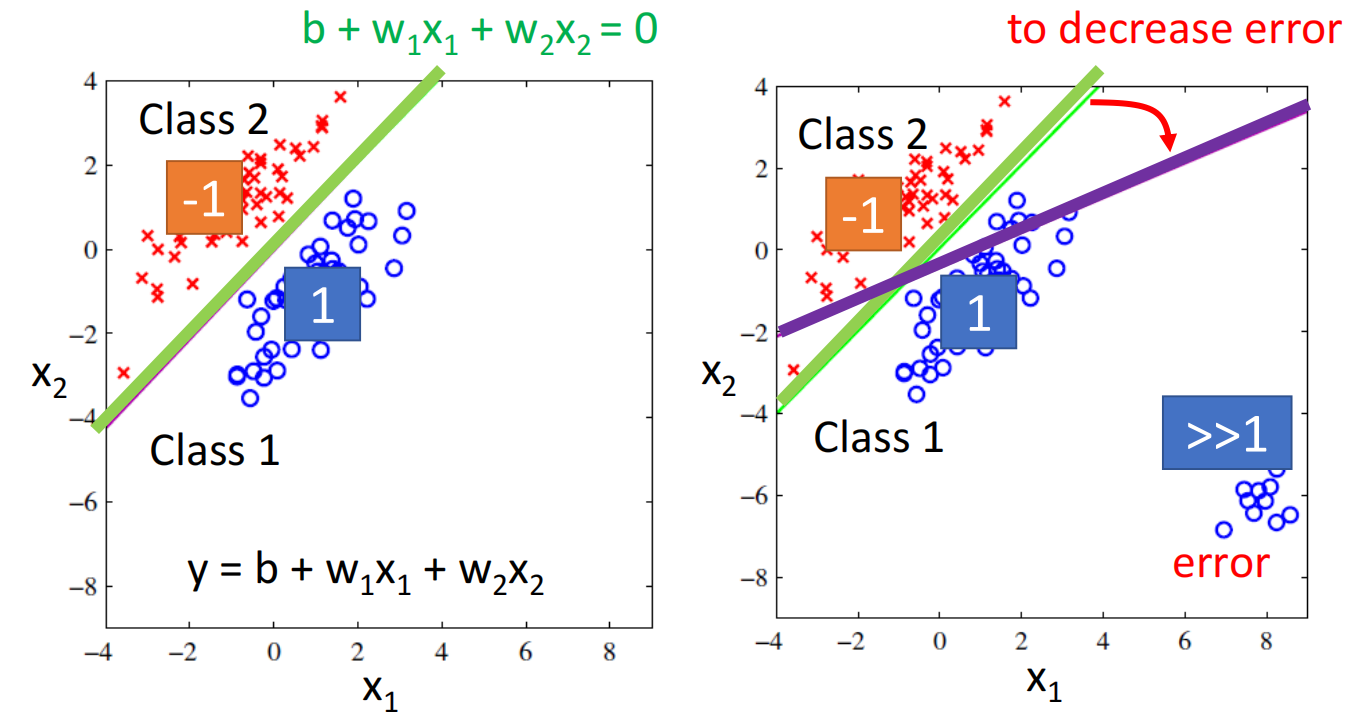
但如果class 1的分布如右图所示，会有部分点远远大于1，而不是接近于1，对于回归来说这些点是不好的，回归此时求最优解也可能会出现紫色结果（因为要减小loss）

补充说明：
分类问题需要去计算数据之间的范数
回归问题所有的数据都需要用相同的范数（同一个赋范空间）去求解
而分类问题可以用在不同的属性之间不同的范数
PS：但在复杂问题中二分类效果其实并不好（SVM不怎么用的原因），此时回归其实效果会更好点的，除非你能建模出一个很好的分类模型
PS：二分类在专家系统里的效果会更好点，在非专家问题中回归可能效果会更好

理想情况下二分类实现方法：

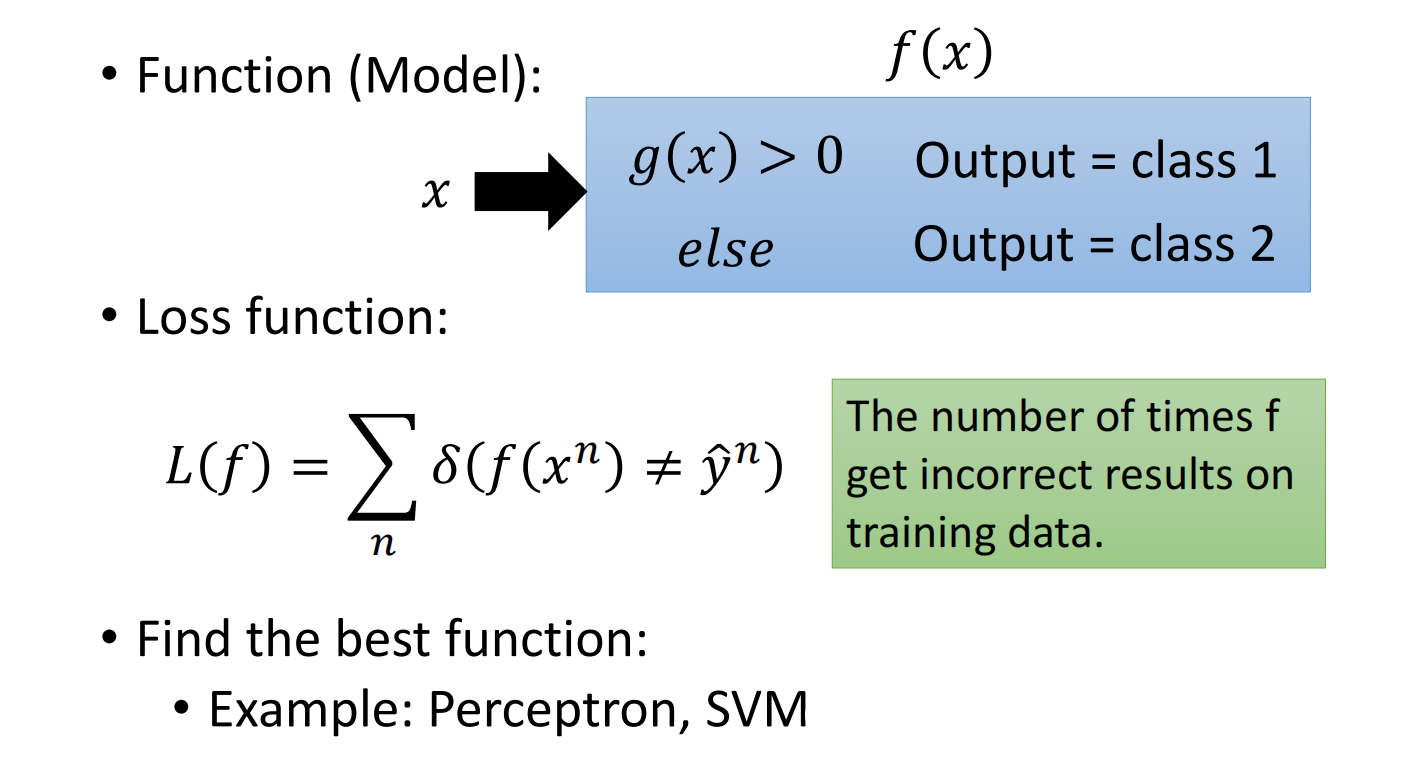
下面先看来另一种方法

生成模型（Generative model）

首先先看条件概率（贝叶斯）

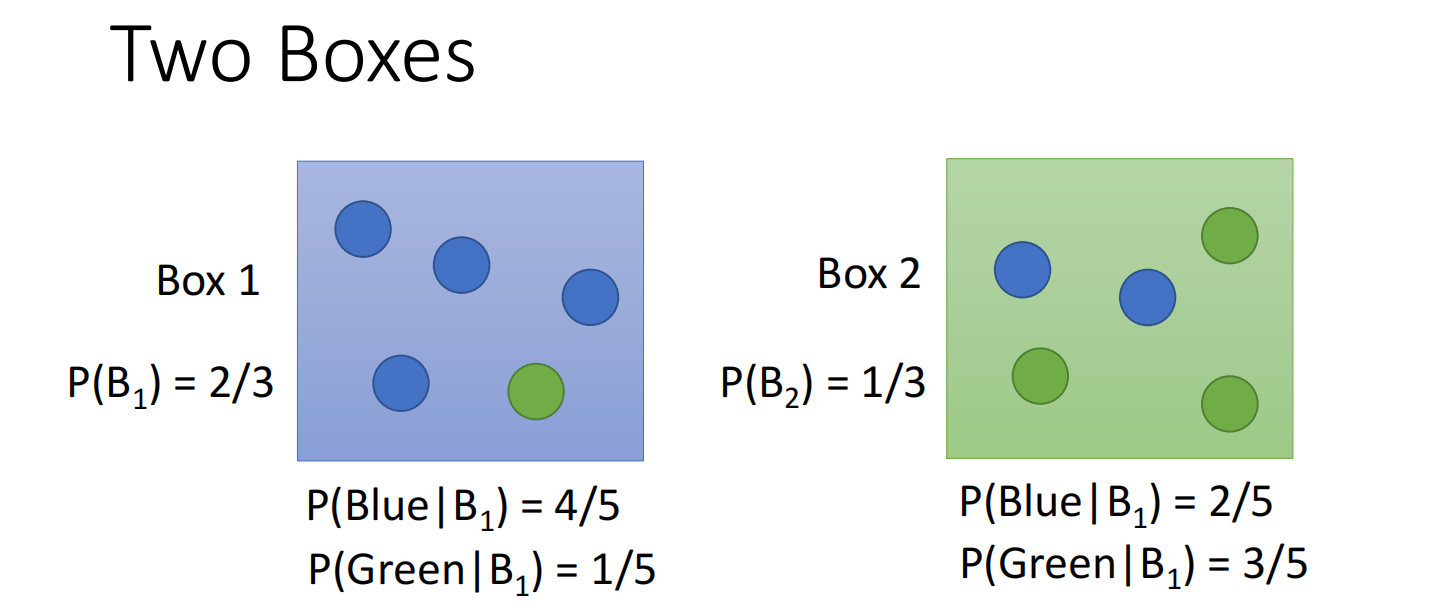
蓝色球从Box1中得到的概率：$\mathrm{P}\left(\mathrm{B}_{1} \mid \text { Blue }\right)=\frac{P\left(\text { Blue } \mid B_{1}\right) P\left(B_{1}\right)}{P\left(\text { Blue } \mid B_{1}\right) P\left(B_{1}\right)+P\left(\text { Blue } \mid B_{2}\right) P\left(B_{2}\right)}$

对于二分类问题来说，给定一个x，判断来源概率为：$P\left(C_{1} \mid x\right)=\frac{P\left(x \mid C_{1}\right) P\left(C_{1}\right)}{P\left(x \mid C_{1}\right) P\left(C_{1}\right)+P\left(x \mid C_{2}\right) P\left(C_{2}\right)}$

生成模型（全概率公式）：$P(x)=P\left(x \mid C_{1}\right) P\left(C_{1}\right)+P\left(x \mid C_{2}\right) P\left(C_{2}\right)$

生成模型解决例子

假设我们得到了一只乌龟，要对这个乌龟进行系别分类，看他它属于水系还是普通系
我们会发现，在我们手中的数据中，可能没有这只乌龟，是不是在这系别中选出该乌龟的概率为0呢？
答案肯定不是，因为我们的数据只是一部分，要得到在指定系别中摇出乌龟的概率，我们要建立一个高斯分布模型，然后通过它来计算。

每一只都是用一个向量来表达，称之为特征（feature）

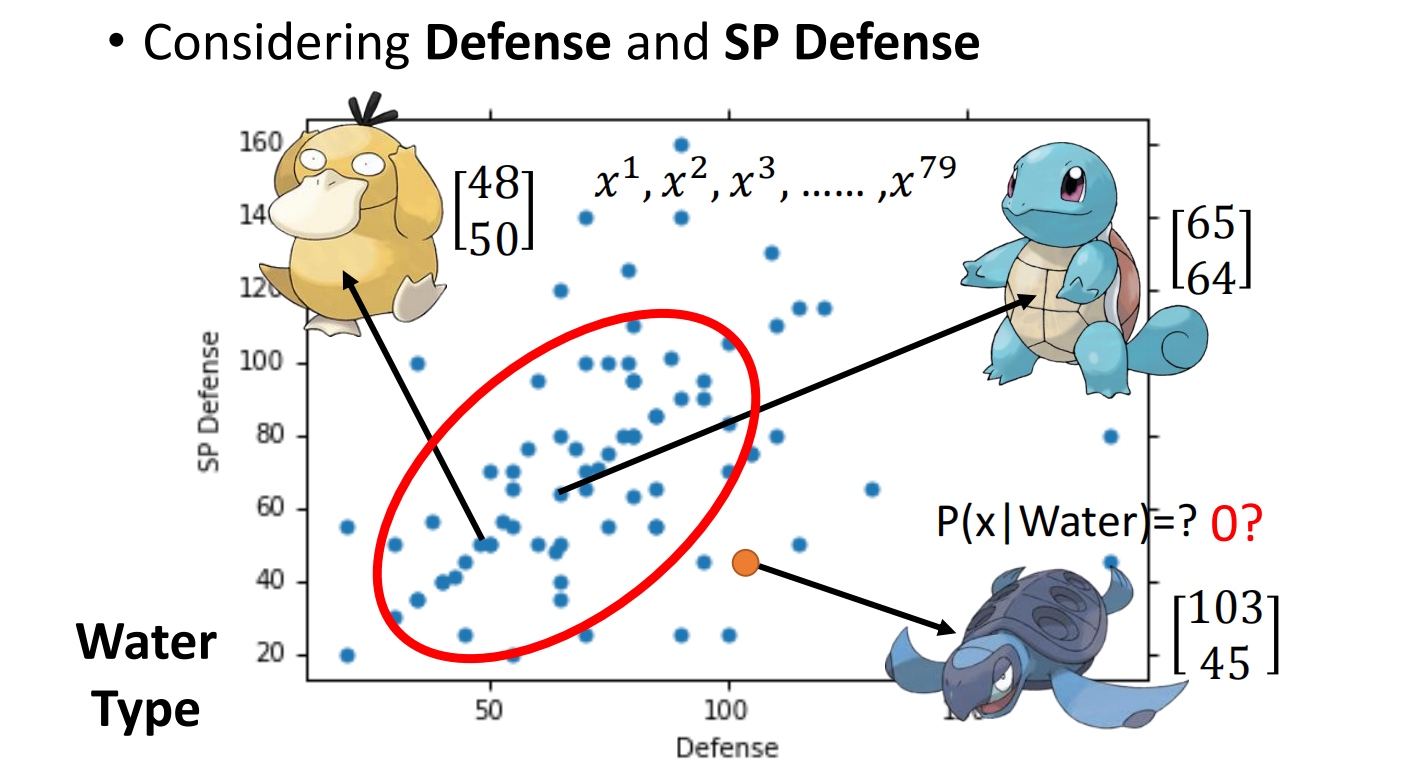
假设水系宝可梦的攻防值是从高斯分布（Gaussian distribution）中抽取出来的

高斯分布：

• $\mu$ 表示的是一个集合的均值
• $\Sigma$ 表示一个集合的方差

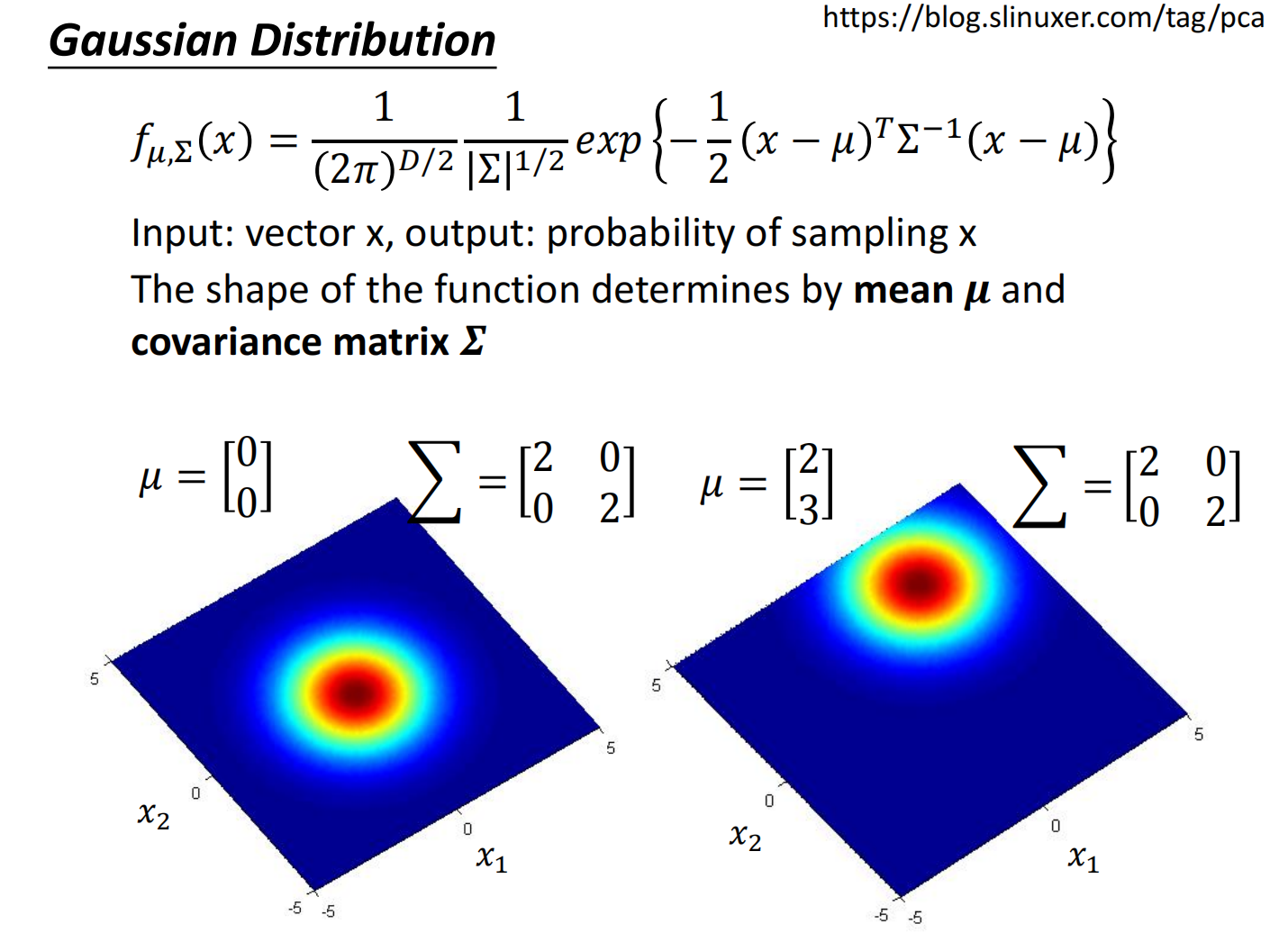
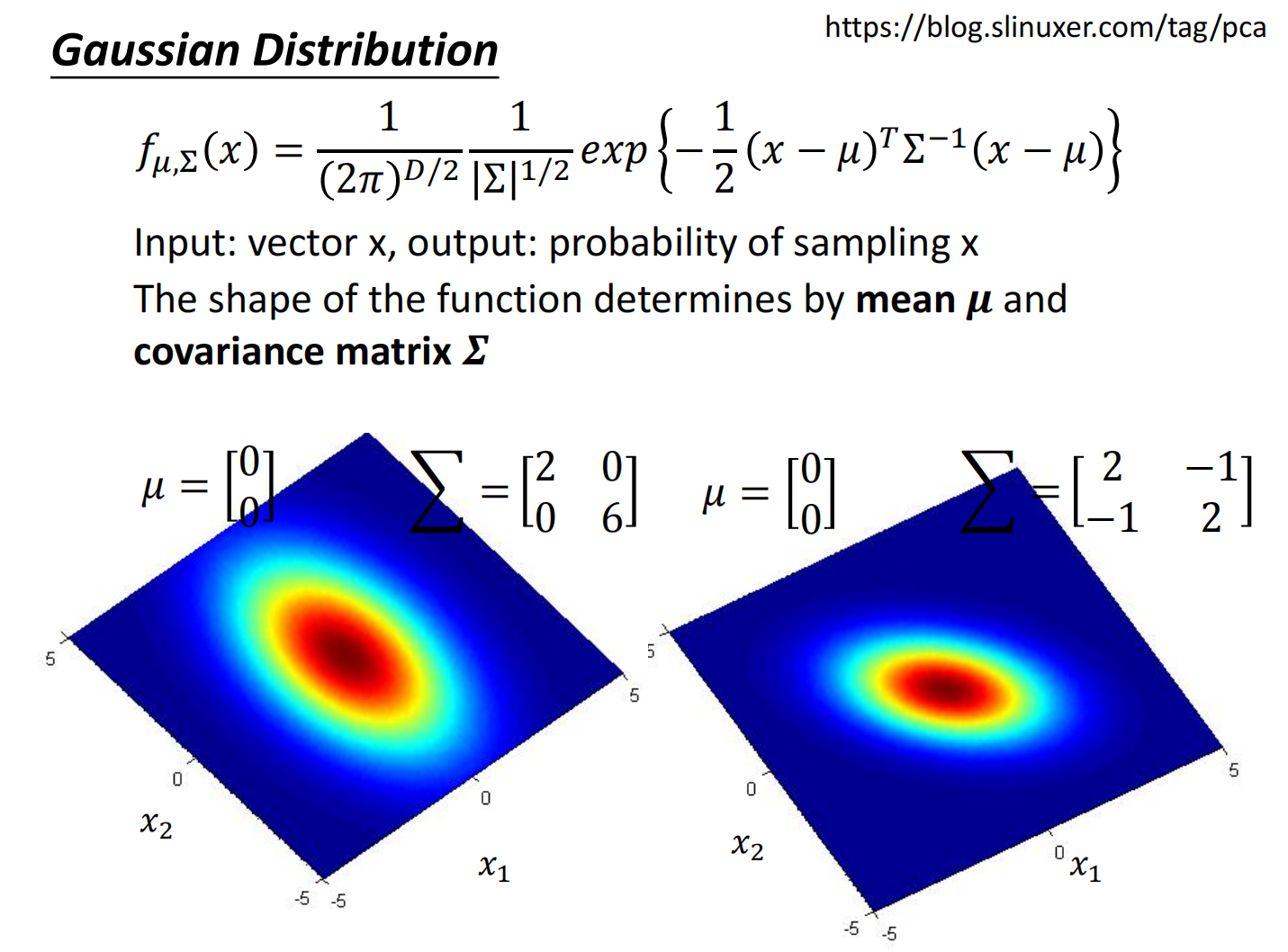
接下来的问题是：我们假设存在一个高斯分布，求出对应的 $\mu$ 和 $\Sigma$

使用极大似然估计（Maximum Likelihood）

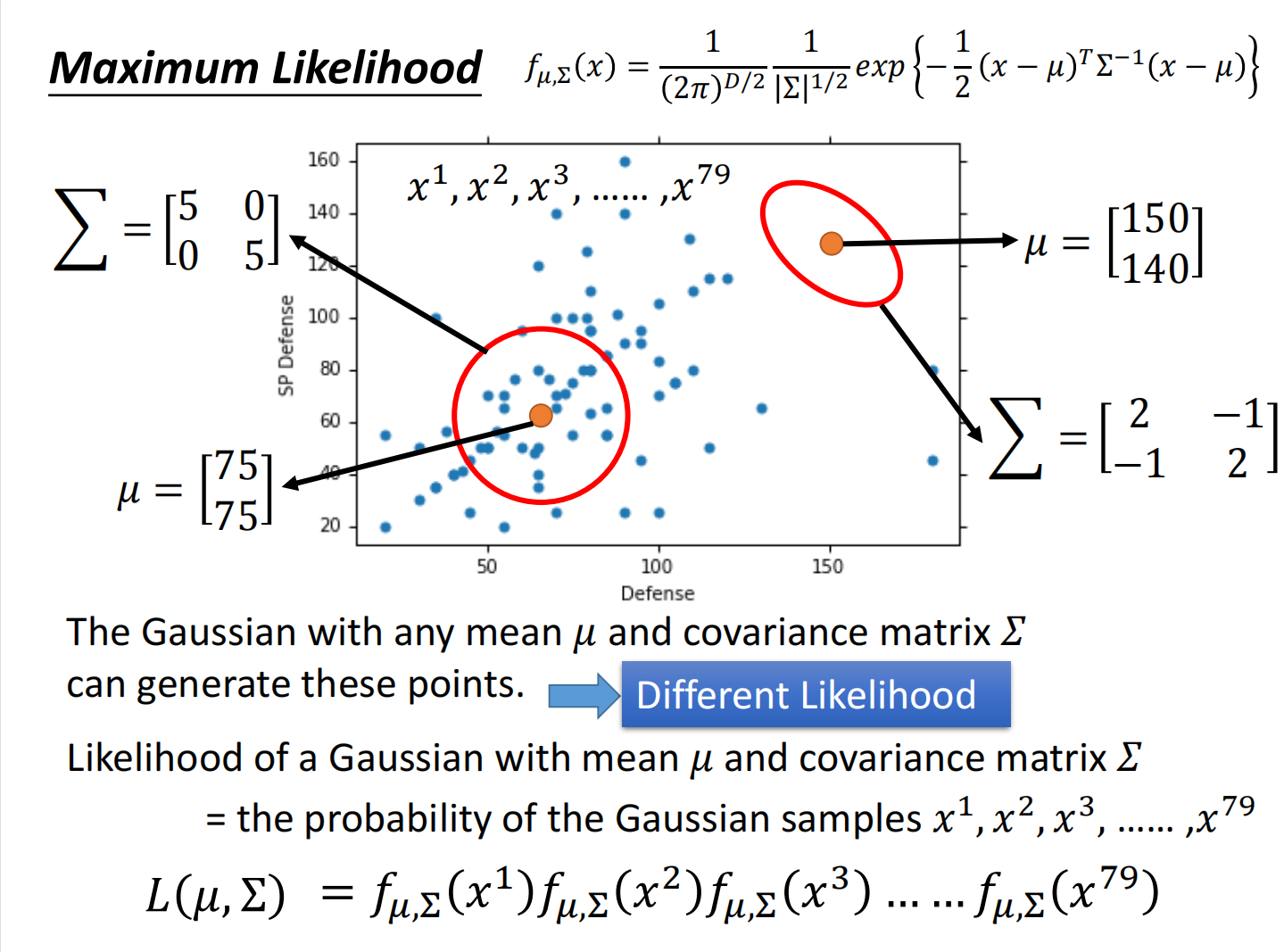
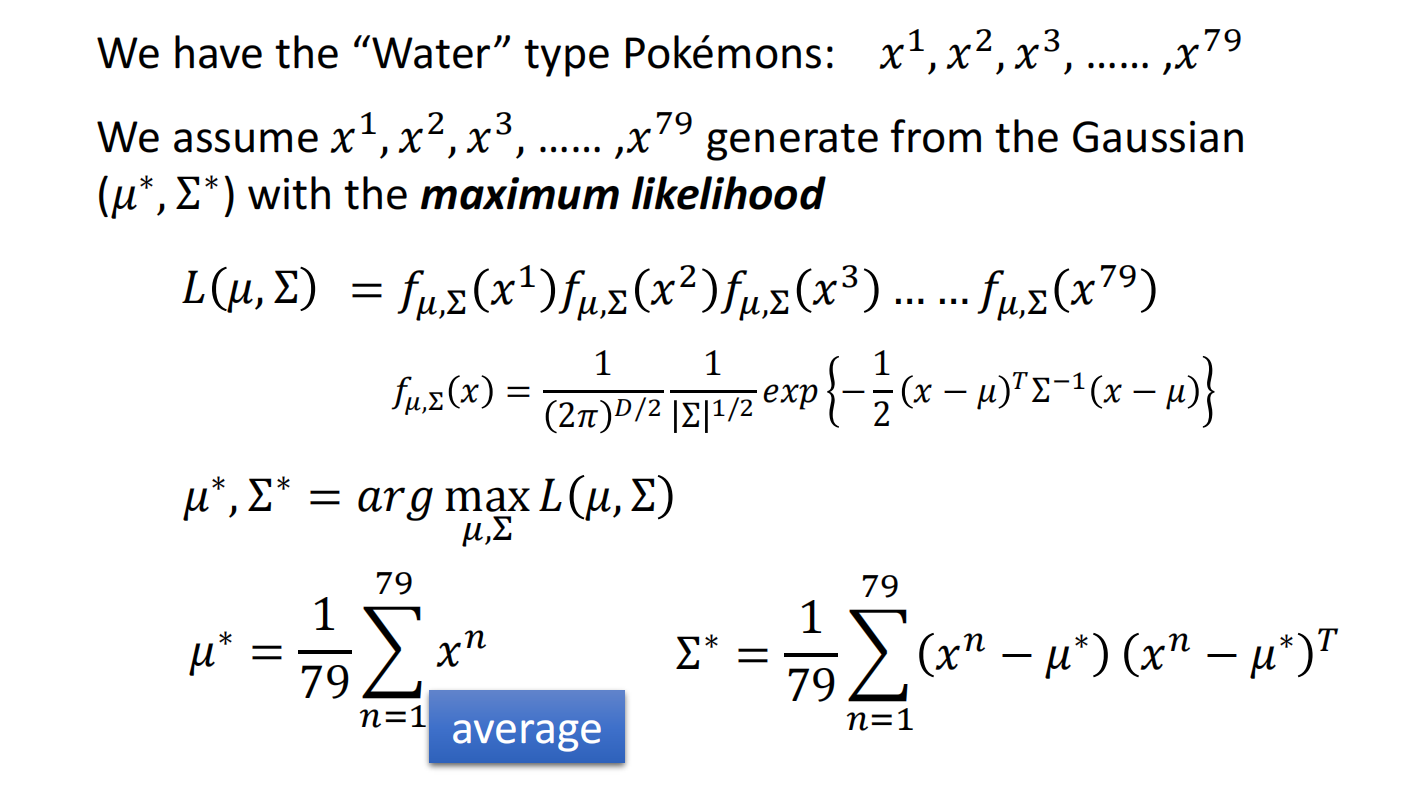
得到结果：

计算分类：

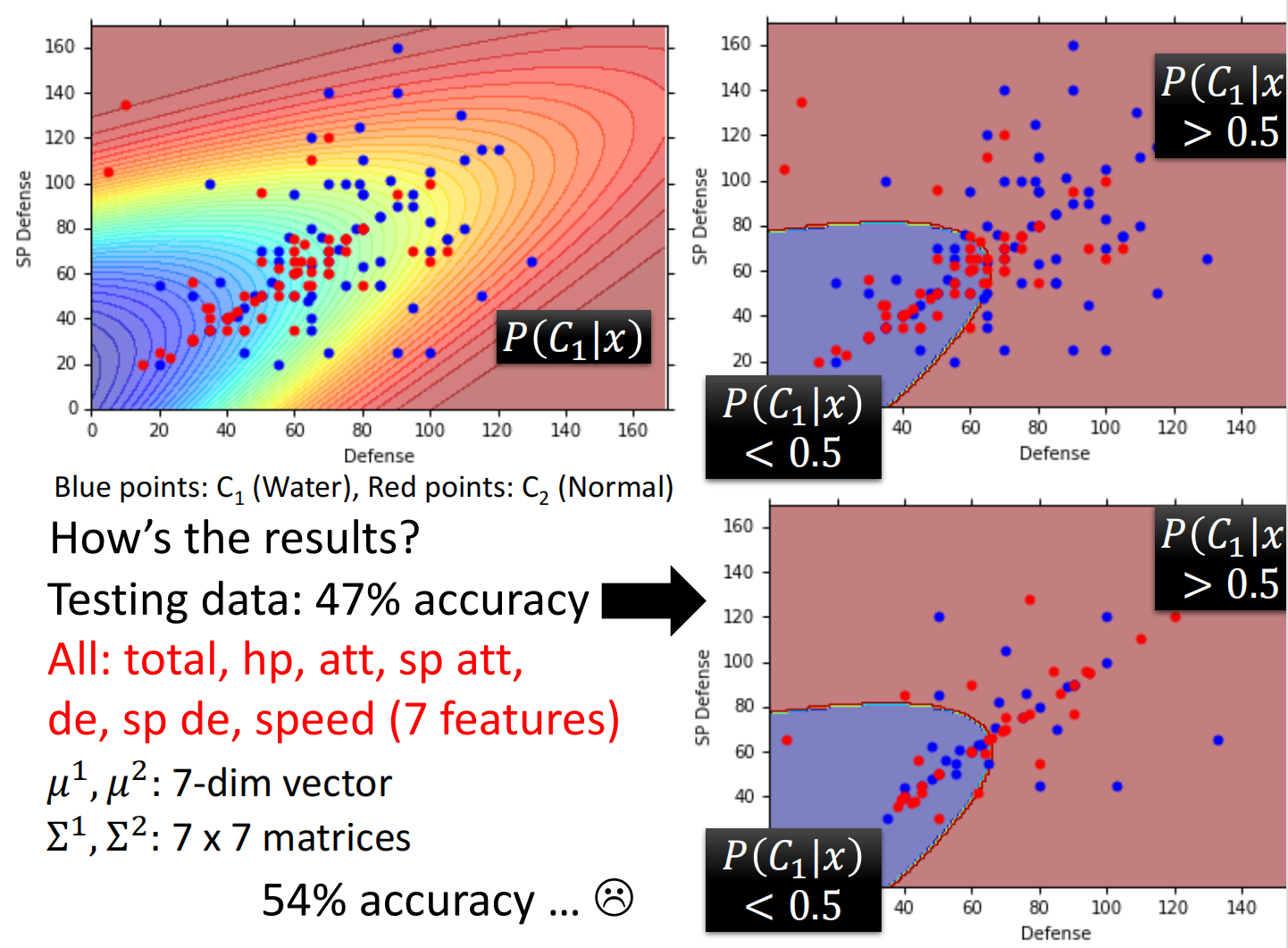
发现结果不太行

那么怎么进行改进呢：
当模型过于复杂的时候，容易过拟合
因此，我们可以让不同类使用同一个 $\Sigma$ ，来减少模型中的参数，进而达到优化目的

可以理解为不管什么系都是宝可梦这大类中的，其服从高斯分布，独立同分布
均值比方差更能代表两组之间的差异，方差主要是显示组内差异

结果：

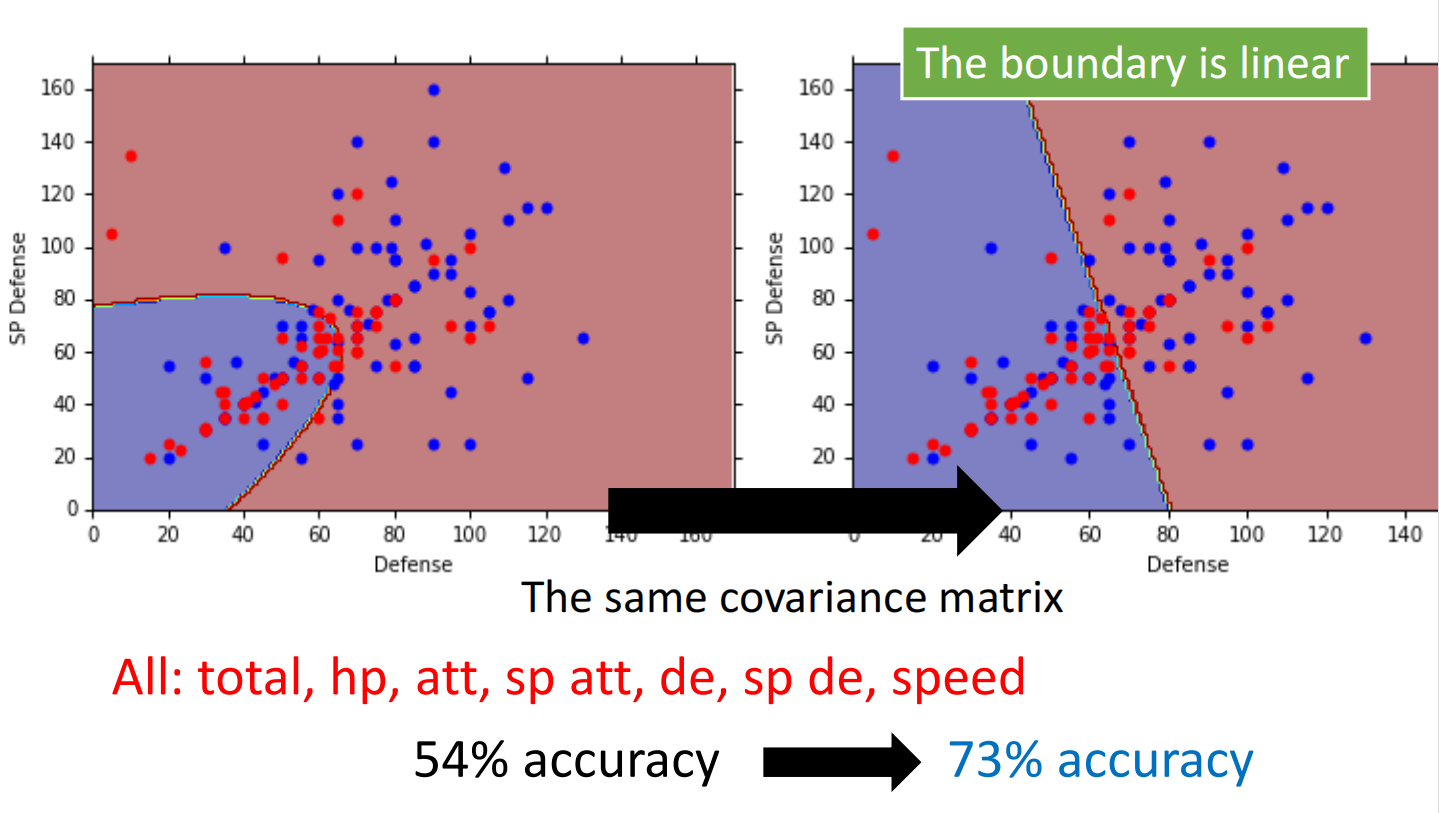
总结

在进行概率计算时，可以把不同特征分开来计算，用他们的乘积来代表一个复合的概率
但是实际上对于我们这个例子来说并不好，因为宝可梦不同特属性之间的相互影响还是比较大的
如果面对一个它的各个特征相互独立的案例，我们分别计算单独特征的概率可能比较简单而且结果也比较好，当然这些要看实际情况

使用同方差，分类为线性边界的原因

首先来设计 $z$ 来简化表达式，使得表达式变为关于 $z$ 的 sigmoid 函数

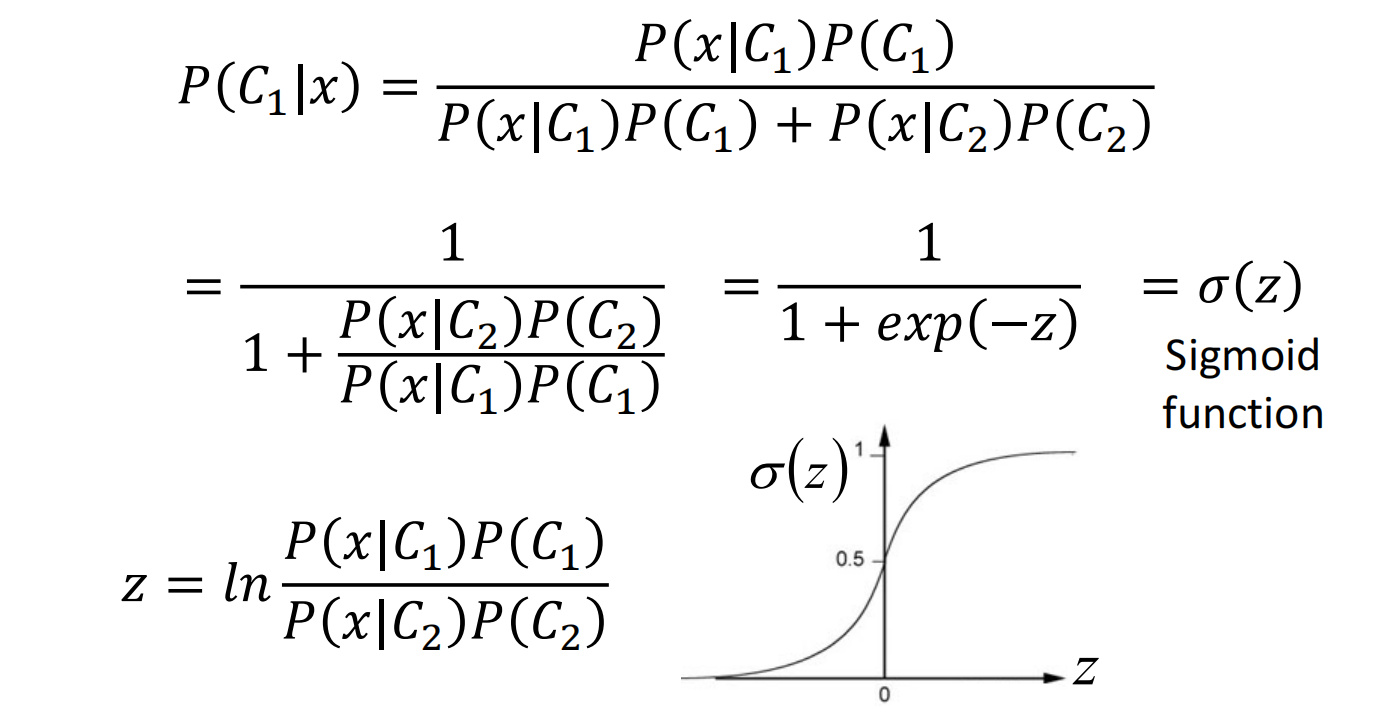
发现确实只有一项与特征值x相关，其余是一个常数，所以结果中的分界线会呈一条直线。

思考：既然最终得出了这样一个表达式，那可不可以直接得出这里的w和b的值，而不去进行上述那些复杂的计算？

这个就是逻辑回归