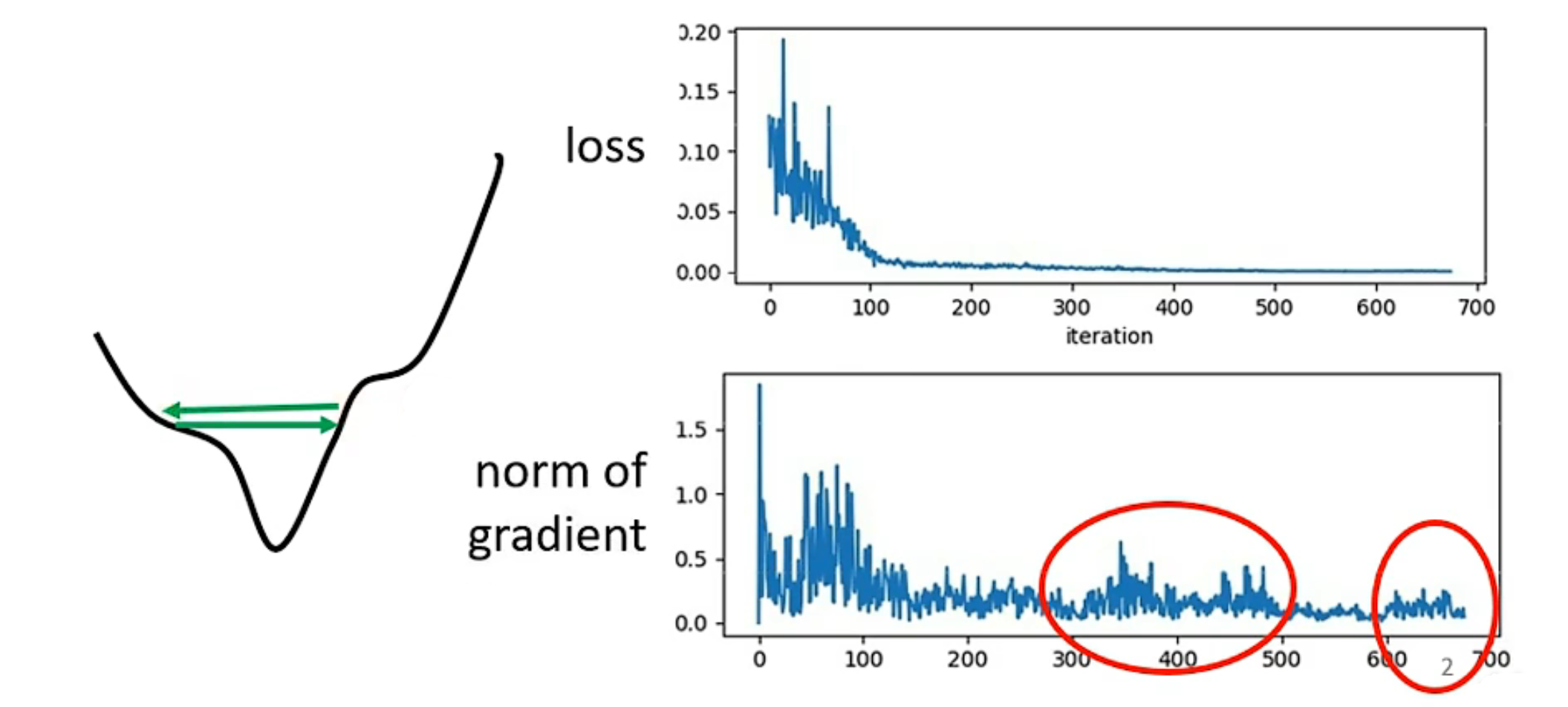
在模型训练过程中,我们可能会遇到模型loss function无法下降的情况，此时梯度为0，这个点统称为临界点（critical point）

局部最小值 (local minima) 与鞍点 (saddle point)

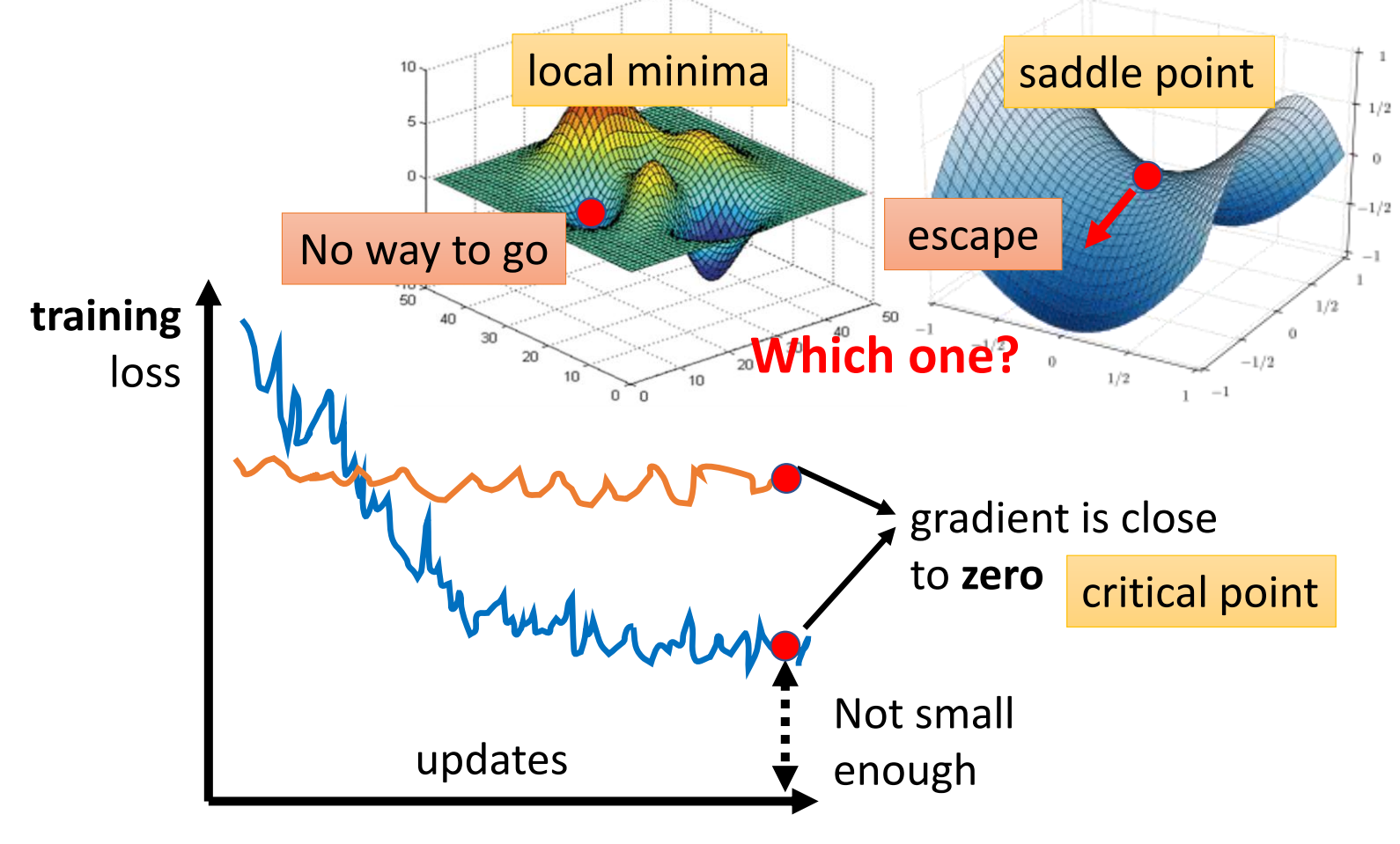
如何判断是卡在局部最小值还是鞍点：调整参数后还能够继续减少就是鞍点

如何解决局部最小值：增加维度，在更高维度中有可能就是saddle point

判断二者如下：

当走到了一个临界点时，gradient=0：

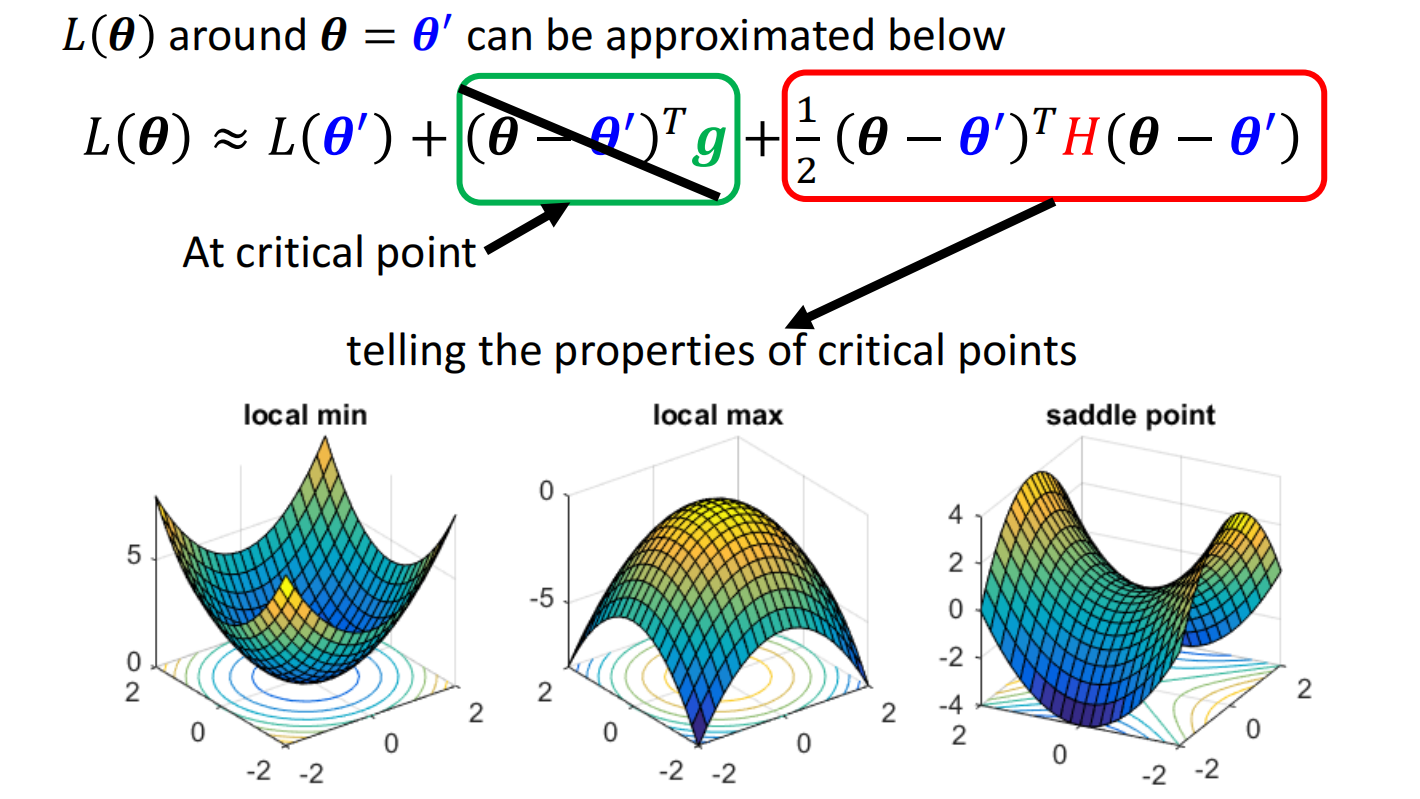
其实可以理解为二阶导判断凹凸性

最后，对于海森矩阵：

• 所有特征值（eigen values）都为正或者都为负 -> 局部最小值
• 特征值有正有负 -> 鞍点

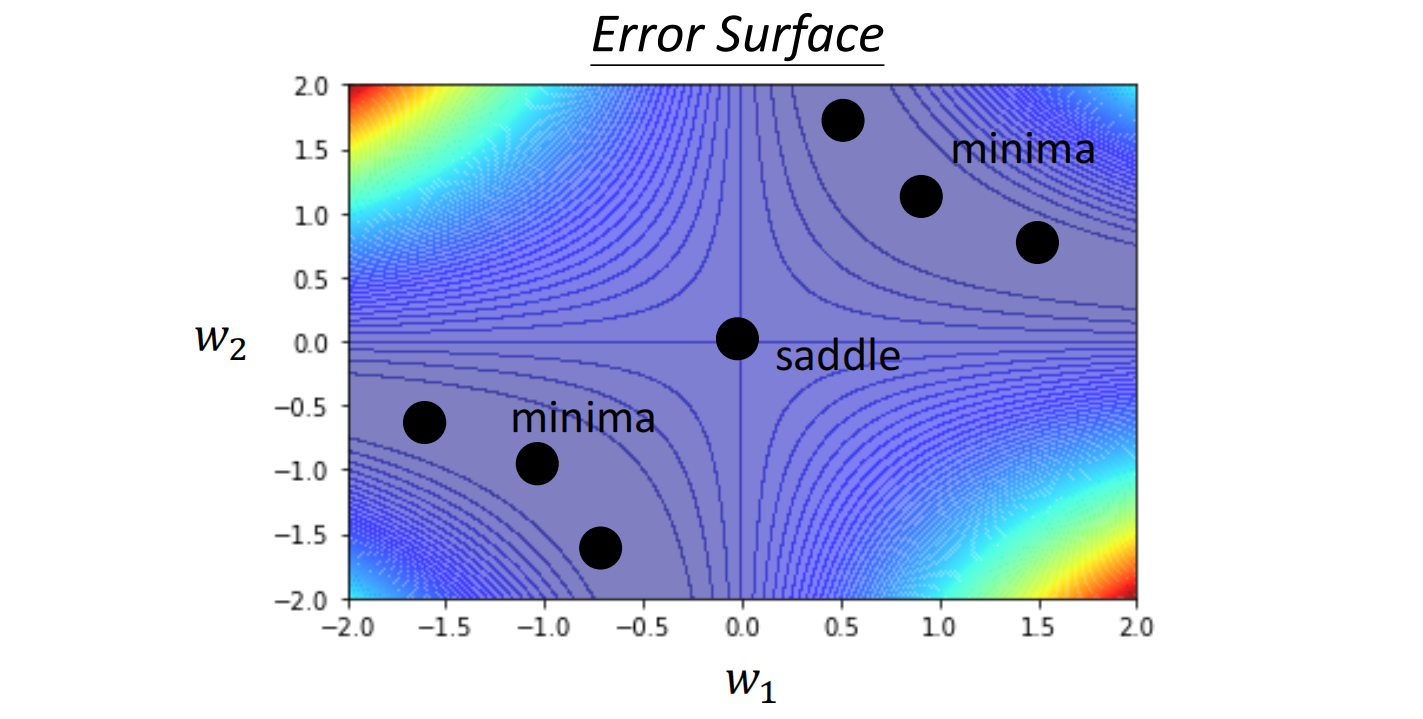
例如：对于此神经网络 $y=w_{1}w_{2}x$，输入1进去，输出越接近1越好

对于所有的Loss function来说，如图所示，存在着鞍点和局部最小值

计算如下：

如果停下来的地方是鞍点，海森矩阵能够给我们提供更新参数的方向

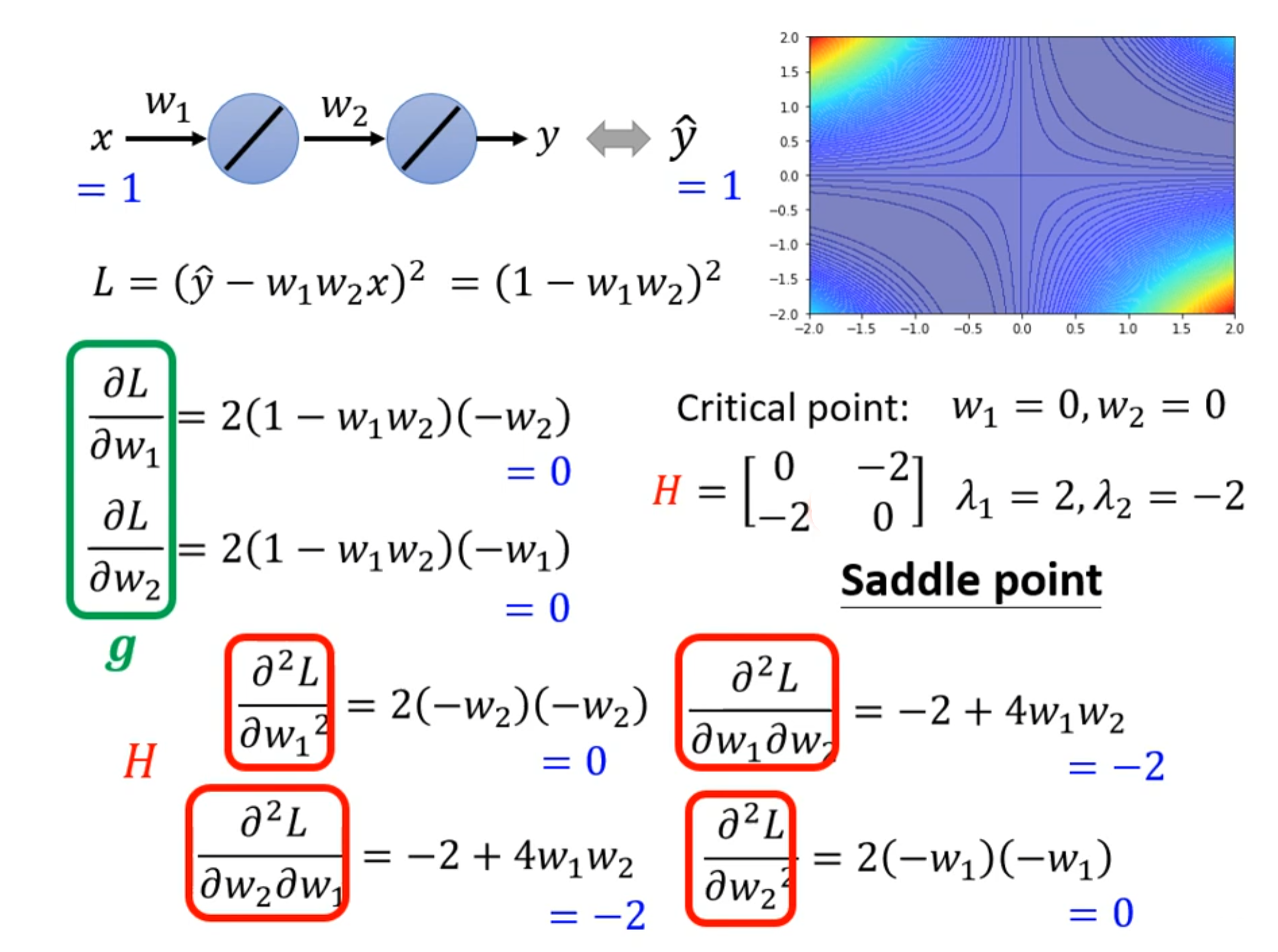
沿着 $u$ 的方向去更新参数，就可以让Loss变小

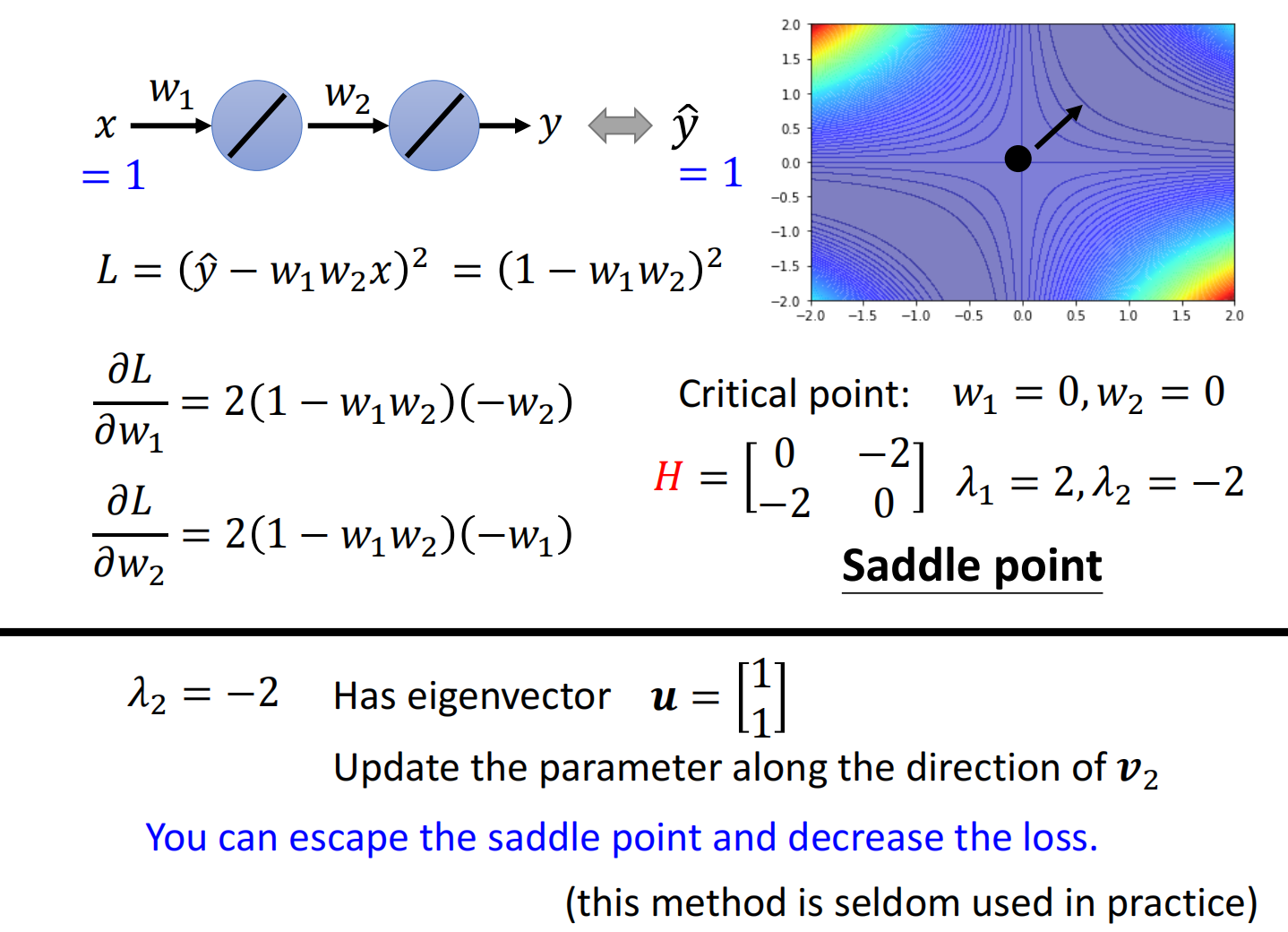
但在实际中，不会真的去算海森矩阵（运算量太大）

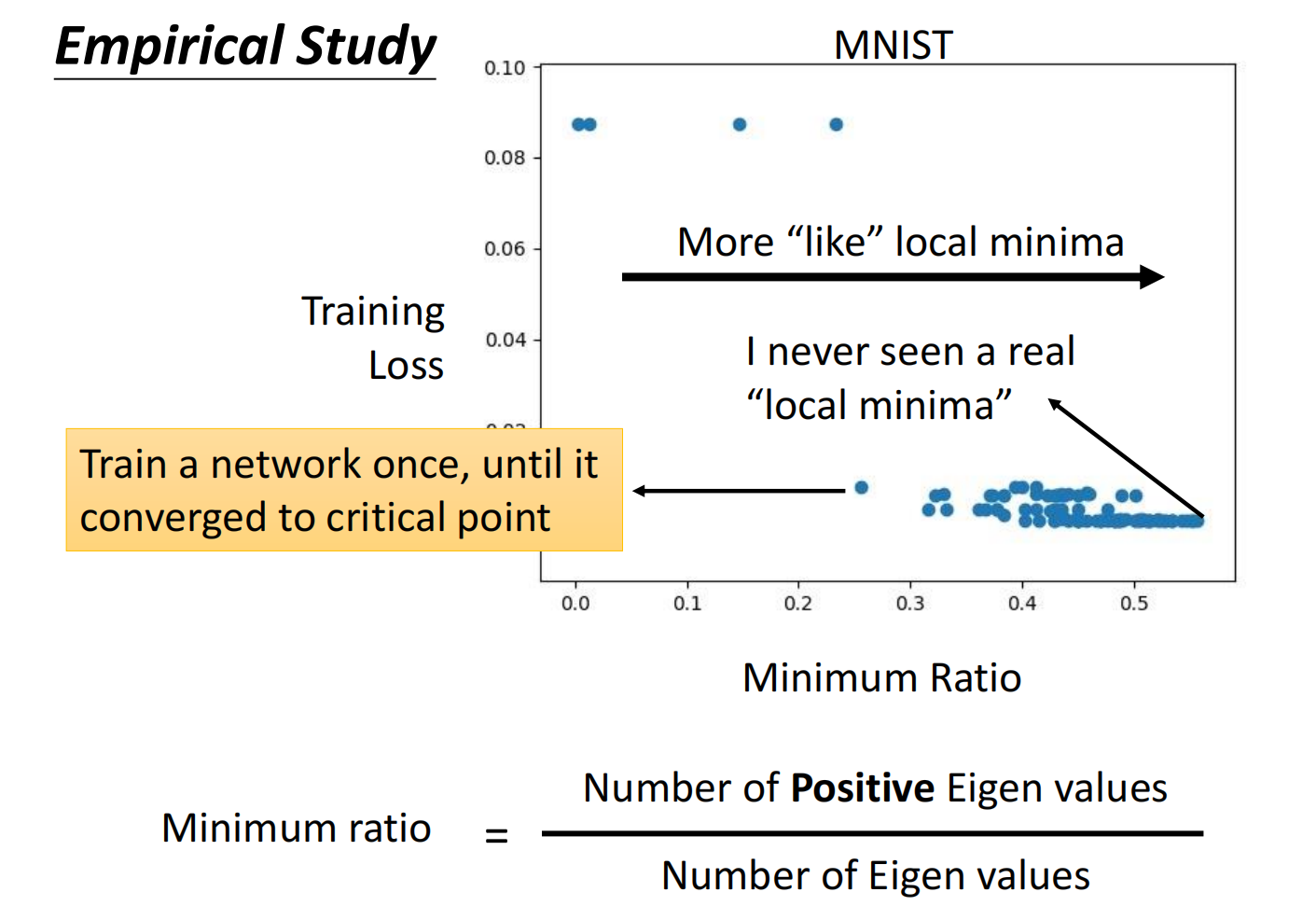
在当前维度的局部最小值，在更高维度会不会是鞍点？
答案是肯定的，从经验上往往是卡在了鞍点，在高纬度中其实没有很多的局部最小值